Средняя арифметическая и средняя квадратическая ошибки

Среднее арифметическое значение серии измерений <X> определяется как частное от деления арифметической суммы всех результатов измерений в серии Xi на общее число измерений в серии n: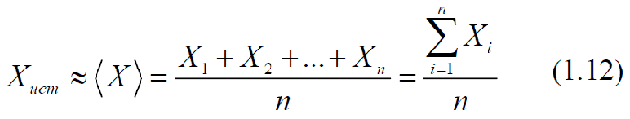

При увеличении n среднее значение <X> стремится к истинному значению измеряемой величины X_ист. Поэтому, за наиболее вероятное значение измеряемой величины следует принять ее среднее арифметическое значение, если ошибки подчиняются нормальному закону распределения ошибок —закону Гаусса.

Формула Гаусса может быть выведена из следующих предположений:

• ошибки измерений могут принимать непрерывный ряд значений;
• при большом числе наблюдений ошибки одинаковой величины, но разного знака встречаются одинаково часто;
• вероятность, то есть относительная частота появления ошибок, уменьшается с увеличением величины ошибки. Иначе говоря, большие ошибки встречаются реже, чем малые.
  

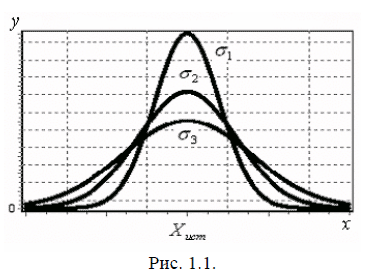
Нормальный закон распределения описывается следующей функцией: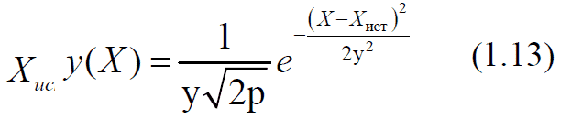

где σ – средняя квадратичная ошибка; σ2 – дисперсия измерения; Х_ист – истинное значение измеряемой величины.

Анализ формулы (1.13) показывает, что функция нормального распределения симметрична относительно прямой X = X_ист и имеет максимум при X = Xист. Значение ординаты этого максимума найдем, поставив в правую часть уравнения (1.13) X_ист вместо X. Получим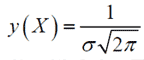

,

откуда следует, что с уменьшением σ возрастает y(X). Площадь под кривой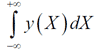

должна оставаться постоянной и равной 1, так как вероятность того, что измеренное значение величины Х будет заключено в интервале от -∞ до +∞ равно 1 (это свойство называется условием нормировки вероятности).

На рис. 1.1 приведены графики трех функций нормального распределения для трех значений σ (σ₃ > σ₂ > σ₁) и одном Х_ист. Нормальное распределение характеризуется двумя параметрами: средним значением случайной величины, которая при бесконечно большом количестве измерений (n → ∞) совпадает с ее истинным значением, и дисперсией σ. Величина σ характеризует разброс погрешностей относительно среднего значения принимаемого за истинное. При малых значениях σ кривые идут более круто и большие значения ΔХ менее вероятны, то есть отклонение результатов измерений от истинного значения величины в этом случае меньше.

Для оценки величины случайной ошибки измерения существует несколько способов. Наиболее распространена оценка с помощью стандартной или среднеквадратичной ошибки. Иногда применяется средняя арифметическая ошибка.

Стандартная ошибка (среднеквадратическая) среднего в серии из n измерений определяется по формуле: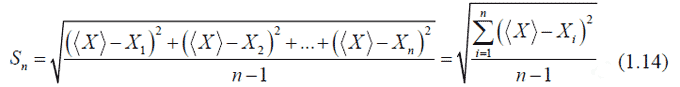

.

Если число наблюдений очень велико, то подверженная случайным случайным колебаниям величина Sn стремится к некоторому постоянному значению σ, которое называется статистическим пределом Sn: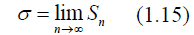

Именно этот предел и называется средней квадратичной ошибкой. Как уже было отмечено выше, квадрат этой величины называется дисперсией измерения, которая входит в формулу Гаусса (1.13).

Величина σ имеет большое практическое значение. Пусть в результате измерений некоторой физической величины нашли среднее арифметическое <Х> и некоторую ошибку ΔX. Если измеряемая величина подвержена случайной ошибке, то нельзя безоговорочно считать, что истинное значение измеряемой величины лежит в интервале (<Х> – ΔХ, <Х> + ΔХ) или (<Х> – ΔХ) < Х < (<Х> + ΔХ)). Всегда существует некоторая вероятность того, что истинное значение лежит за пределами этого интервала.

Доверительным интервалом называется интервал значений (<Х> – ΔХ, <Х> + ΔХ) величины X, в который по определению попадает ee истинное значение Х_ист с заданной вероятностью.

Надежностью результата серии измерений называют вероятность того, что истинное значение измеряемой величины попадает в данный доверительный интервал. Надежность результата измерения или доверительная вероятность выражается в долях единицы или процентах.

Пусть α означает вероятность того, что результат измерений отличается от истинного значения на величину, не большую, чем ΔХ. Это принято записывать в виде:

Р((<Х> – ΔХ) < Х < (<Х> + ΔХ)) = α

Выражение (1.16) означает, что с вероятностью, равной α, результат измерений не выходит за пределы доверительного интервала от <Х> – ΔХ до <Х> + ΔХ. Чем больше доверительный интервал, то есть чем больше задаваемая погрешность результата измерений ΔХ, тем с большей надежностью искомая величина Х попадает в этот интервал. Естественно, что величина α зависит от числа n произведенных измерений. а также от задаваемой погрешности ΔХ.

Таким образом, для характеристики величины случайной ошибки, необходимо задать два числа, а именно:

• величину самой ошибки (или доверительный интервал);
• величину доверительной вероятности (надежности).

Указание одной только величины ошибки без указания соответствующей ей доверительной вероятности в значительной мере лишено смысла, так как при этом мы не знаем, сколь надежны наши данные. Знание доверительной вероятности позволяет оценить степень надежности полученного результата.

Необходимая степень надежности задается характером проводимых изменений. Средней квадратичной ошибке S_n соответствует доверительная вероятность 0.68, удвоенной средней квадратичной ошибке (2σ) – доверительная вероятность 0.95, утроенной (3σ) – 0.997.

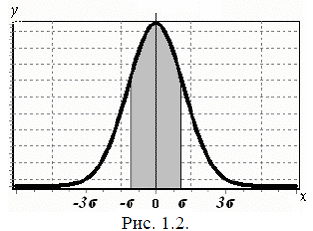
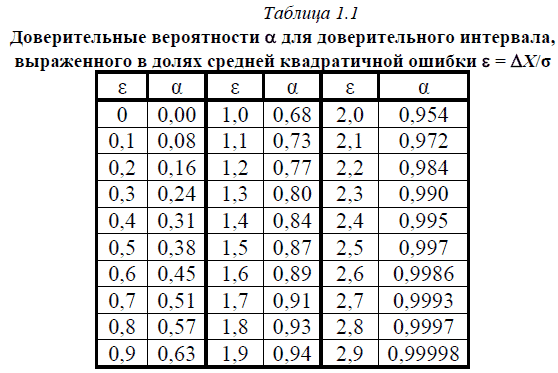
Если в качестве доверительного интервала выбран интервал (X – σ, X + σ), то мы можем сказать, что из ста результатов измерений 68 будут обязательно находиться внутри этого интервала (рис. 1.2). Если при измерении абсолютная погрешность ∆Х > 3σ, то это измерение стоит отнести к грубым погрешностям или промаху. Величину 3σ обычно принимают за предельную абсолютную погрешность отдельного измерения (иногда вместо 3σ берут абсолютную погрешность измерительного прибора).

Для любой величины доверительного интервала по формуле Гаусса может быть рассчитана соответствующая доверительная вероятность. Эти вычисления проведены и их результаты сведены в табл. 1.1.

Доверительные вероятности α для доверительного интервала, выраженного а долях средней квадратичной ошибки ε = ΔX/σ: