«Водородоподобные атомы» в классической механике. Теория Бора
|
4.2.1. Линейчатые спектры атомов
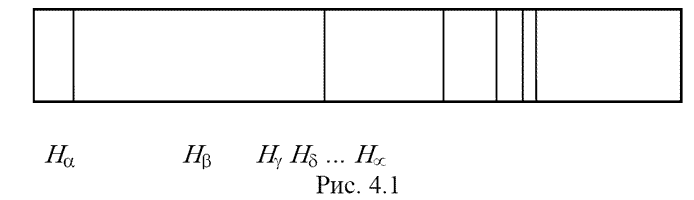
Спектры испускания невзаимодействующих друг с другом атомов имеют дискретный характер, то есть состоят из более или менее узких спектральных линий. Такие спектры называются линейчатыми. Спектральные линии образуют группы - так называемые серии. Наиболее простой линейчатый спектр даёт атомарный водород. Спектр водорода состоит из нескольких серий:
Линии серии Бальмера обозначаются символами Нα , Нβ , Нγ , Нδ ... Длины волн (и соответственно, частоты) спектральных линий водорода подчиняются определённым закономерностям, выраженным формулой Бальмера: 1 / λ = R* ( 1 / (n2)2 - 1 / (n1)2 ) (4.1) где R - постоянная Ридберга, названная в честь шведского ученого, который определил её значение опытным путем; n2 и n1 - целые числа, причём n2 имеет в каждой серии постоянное значение, а n1 - принимает ряд целых значений, начинающихся с числа, на единицу большего n2. Для серии Лаймана n2 = 1, n1 = 2, 3, 4 и т.д. Для серии Бальмера n2 = 2, n1 = 3, 4, 5 и т.д. В соответствии с этим длины волн спектральных линий серии Бальмера определяются по формуле: 1 / λ = R* ( 1 / (2)2 - 1 / (n1)2 ), где n1 = 3,4,5, ...
(4.2) Максимальная частота (минимальная длина волны) при n1 = ∞ называется границей серии. Наличие множества спектральных линий указывает на сложность внутренней структуры атомов. 4.2.2. «Водородоподобные атомы» в классической механике В 1911 году английским ученым Резерфордом была предложена теория строения атома любого химического элемента. Согласно этой теории атом состоит из положительно заряженного ядра и движущихся вокруг ядра отрицательных электронов. Суммарный заряд электронов по абсолютной величине равен заряду ядра, так что атом в целом нейтрален. Ядро занимает ничтожную часть объёма атома, но в нём сосредоточена почти вся масса атома. Рассмотрим атом водорода и «водородоподобные атомы», то есть ионы, состоящие из ядра с зарядом +Ze (Z - порядковый номер атома в таблице Менделеева) и только одного обращающегося вокруг ядра электрона. Второй закон Ньютона для электрона, движущегося в поле ядра под действием кулоновской силы, имеет вид mev2 / r = ( 1 / 4πε0 ) * ( Ze2 / r2 ) (4.3) где me - масса электрона, v - скорость движения электрона по орбите, r - радиус орбиты, εem0 - электрическая постоянная, 1 / 4πε0 - коэффициент для согласования величин в СИ, Z - порядковый номер элемента в таблице Менделеева, Zе - заряд ядра. Отсюда кинетическая энергия электрона в атоме W = mev2 / r = ( 1 / 8πε0 )*( Ze2 / r ) (4.4) C другой стороны, электрон в электрическом поле ядра обладает потенциальной энергией U. Принято считать, что потенциальная энергия свободного электрона (вырванного из атома), равна нулю, тогда в пределах атома U < 0, или U = - ( Ze2 / 4*π*r*ε0 ) (4.5) Полная энергия электрона выразится суммой его кинетической и потенциальной энергий, то есть E = W + U или E = ( 1 / 8πε0 )*( Ze2 / r ) - ( Ze2 / 4*π*r*ε0 ) = - ( 1 / 8πε0 )*( Ze2 / r ) (4.6) Из классической электромагнитной теории следует, что движущийся с ускорением по орбите электрон должен излучать электромагнитные волны. Из-за потери энергии на излучение радиус его орбиты должен непрерывно уменьшаться (формула 4.6), и, в конце концов, электрон должен упасть на ядро, то есть атом перестанет существовать. В действительности атом является устойчивой системой. Это одно из основных противоречий классической теории. Другое противоречие этой теории состоит в том, что с уменьшением радиуса орбиты линейная скорость электрона должна возрастать (формула 4.4), т.е. частота обращения электрона должна увеличиваться. Если считать, что частота обращения, следовательно, и частота излучения электрона, непрерывно растёт, то спектры атомов должны быть сплошными. В действительности, как уже было сказано, спектры невзаимодействующих атомов имеют линейчатый характер. Это указывает на то, что процессам внутри атомов свойственна прерывность или дискретность. 4.2.3. Теория строения атома по Бору Теоретическое объяснение спектральных закономерностей было впервые дано в полуклассической теории Бора. Нильс Бор, используя планетарную модель атома Резерфорда и основываясь на дискретном характере излучения и квантовой гипотезе Планка, сформулировал следующие постулаты: Первый постулат Бора (постулат стационарных состояний): В атоме существуют стационарные (не изменяющиеся со временем) состояния, в которых он не излучает энергию. Стационарным состояниям атома соответствуют стационарные орбиты, по которым движутся электроны. Правило квантования орбит Бора утверждает, что в стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь квантованные значения момента импульса, то есть удовлетворяющие условию: Ln = me*v*r = n*ђ = n*h/(2π), (4.7) где me - масса электрона,v - скорость движения электрона по орбите, r - радиус орбиты, n - целое число, n = 1, 2, ..., ђ - постоянная Планка, ђ = h/2π. Второй постулат Бора (правило частот) устанавливает, что при переходе атома из одного стационарного состояния в другое испускается или поглощается один фотон. Энергия фотона равна разности энергий тех стационарных состояний, между которыми совершается квантовый переход: h*ν = ђ*ω = En2 - En1 (4.8) где ω = 2πν - круговая частота фотона.При Еn2 > En1 происходит поглощение фотона, при Еn2 < En1 - излучение его. Хотя постулаты Бора и противоречат классической физике, но определение радиуса орбиты электрона и его энергии на этой орбите ведется методом классической физики. Именно поэтому теорию Бора называют полуклассической. Решая совместно уравнение движения электрона в поле атомного ядра (4.3) и уравнение (4.7), выражающее правило квантования орбит, (исключая из них ) получим выражение для радиусов орбит стационарных состояний: rn = ( h2 * ε0 / ( π*me*e2 ) ) = 0,529*10-10 м (4.10) Внутренняя энергия атома складывается из кинетической энергии электрона (ядро считаем неподвижным) и энергии взаимодействия электрона с ядром и определяется выражением (4.6). Подставив в (4.6) выражение (4.9) для r, найдём допустимые значения внутренней энергии атома: En = - (me * Z2 * e4) / ( 8 * (ε0)2 * n2 * h2 ) ( n = 1, 2, 3, ... ) (4.11) Совокупность значений энергии стационарных состояний атома Е1, Е2, Е3, ... образует энергетический спектр атома. Каждое значение энергии в нём называется уровнем энергии. Низший уровень Е1 называется основным, а все остальные − возбуждёнными. Зависимость энергии атома от n можно показать на диаграмме энергетических уровней, где по одной из осей отложены значения энергии Еn (рис. 4.2). Энергетический уровень − условное обозначение горизонтальной линией соответствующего значения Еn. Изменения энергии электрона при переходе между состояниями символически изображены на диаграмме стрелками, проведенными из начального состояния в конечное. Переходу электрона с уровня n1 на уровень n2 соответствует поглощение (n2 > n1) или излучение (n2 < n1) фотона с частотой ν = ( En1 - En2 ) / h = ( me * e4 ) / ( 8*(ε0)2 * h3) * ( 1 / (n22) - 1 / (n12) ) Или, учитывая что ν = с/λ, получим формулу Бальмера(4.12) 1 / λ = R* ( 1 / (n22) - 1 / (n12) ) (4.13) где R - постоянная Ридберга: R = ( me * e4 ) / ( 8*(ε0)2 * h3 * c) (4.14) 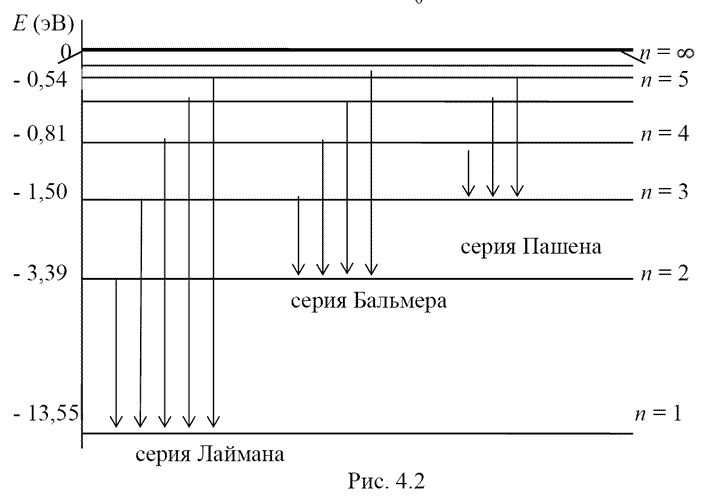 Если определяют длину волны (формула 4.13), то численное значение постоянной Ридберга R = 1,09737 * 107 м−1. Если определяют частоту ν = c/λ: ν = R' * ( 1 / (n22) - 1 / (n12) ) где R' = 3,28985*1015 Гц (R' = R*c, c = 3 ⋅ 108 м/с).(4.15) Если определяют круговую частоту ω = 2πν: ω = R'' * ( 1 / (n22) - 1 / (n12) ) (4.16) где R′′ = 2πR′ = 2,07 ⋅ 1016 c−1.Вычисленное по формуле (4.14) и экспериментальное значение постоянной Ридберга совпадают. Таким образом, планетарная модель атома и теория Бора дают хорошие результаты в случае атома водорода. Однако спектральные закономерности более сложных атомов (Z > 1) теория Бора объяснить не может. Наиболее полное и точное решение задачи о спектральных закономерностях даёт квантовая механика. Автор методики: Андреева И.В; ВолгГТУ Добавил: COBA (02.03.2010) | Категория: Квантовая физика Просмотров: 11374 | Загрузок: 1 | Рейтинг: 0.0/0 | Теги: |
| Комментарии (0) | |