Определение доверительного интервала и доверительной вероятности
|
Ранее нами было рассмотрено определение доверительной вероятности для отдельного измерения Xi с помощью табл. 1.1, то есть определение вероятности того, что Xi не будет отклоняться от истинного значения более чем на величину ΔX.
Однако, наиболее важной задачей является определение величины отклонения от истинного значения Xист среднего арифметического <X> результатов измерений. Для решения поставленной задачи также можно воспользоваться табл. 1.1, взяв, вместо величины σ величину σ<X>, то есть у / (n0.5) или с учетом (1.14), для конечного числа измерений 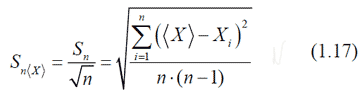 Средняя квадратичная ошибка среднего арифметического Sn<X> равна средней квадратичной ошибке отдельного результата, деленой на корень квадратный из числа измерений. Это фундаментальный закон возрастания точности при росте наблюдений. Из него следует, что для повышения точности измерений в 2 раза необходимо увеличить число измерений в 4 раза. Однако этот вывод относится только к измерениям, в которых точность результата полностью определяется случайной ошибкой. Обычно выполняется сравнительно небольшое число измерений для n которых определяется величина Sn<X>. Если при оценке доверительной вероятности считать, что значение Sn<X> совпадает с у<X> и пользоваться табл. 1.1, то будем получать завышенные значения α. Из того, что σ<X> является пределом Sn<X> при n → ∞, следует, что Sn<X> пропорциональна величине σ<X>. Коэффициент пропорциональности зависит от числа измерений и отражает степень приближения Sn<X> к σ<X>. На основании этого интервал ΔX можно представить в виде 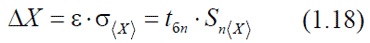 Значения величины tαn, носящей название коэффициента Стьюдента, вычислены для различных значений n и α и приведены в табл. 1.2. Сравнивая приведенные в ней данные с данными табл. 1.1, легко убедиться, что при больших n величина tαn стремится к соответствующим значениям величины ε. Это естественно, так как с увеличением n Sn<X> стремится к σ<X>. 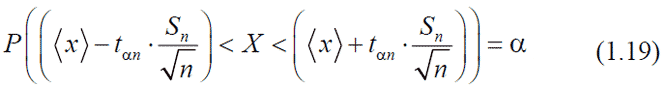 Пользуясь этим соотношением и табл. 1.2, легко определить доверительные интервалы и доверительные вероятности при любом небольшом числе измерений. После выполнения измерений должны быть известны все величины, входящие в это выражение - одни из них могут быть наперед заданы, другие необходимо определить. Мерой точности результатов измерений является относительная погрешность (ошибка), обычно выражаемая в процентах (%): 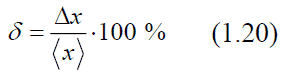 Величину ϕ = 1/δ, обратную относительной погрешности называют точностью измерений. Таблица коэффициентов Стьюдента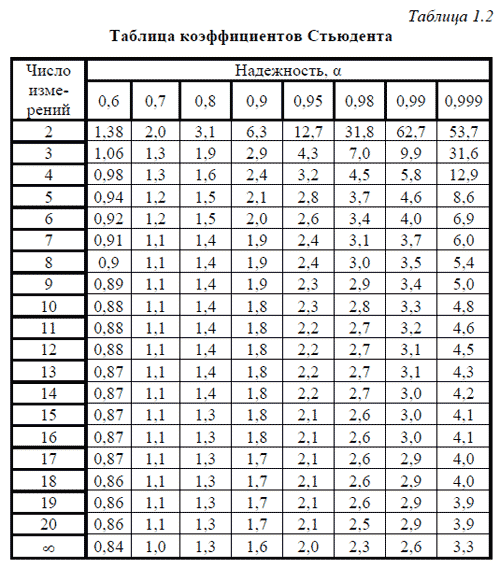 Добавил: mauzer (04.12.2011) | Категория: Механика Просмотров: 27140 | Загрузок: 0 | Рейтинг: 4.0/1 | |
| Комментарии (0) | |
