Спонтанные и индуцированные переходы
|
Примечание: r' и k' - являются векторами r и k соответственно.
Один из основных выводов квантовой механики гласит, что каждая физическая система (например, электрон в атоме) может находиться только в одном из заданных энергетических состояний, - так называемых, собственных состояниях системы.
С каждым состоянием (скажем, с состоянием электрона) можно связать собственную функцию
Ψ ( r' , t ) = Un * ( r' ) * e-iEnt/ħ
причем | Un (r') | 2 dxdydz - вероятность нахождения электрона в некотором состоянии n в
пределах элементарного объема dxdydz с центром в точке, определяемой радиус-вектором r'
, Еn - энергия n -го состояния, ħ = h/2π; - постоянная Планка.
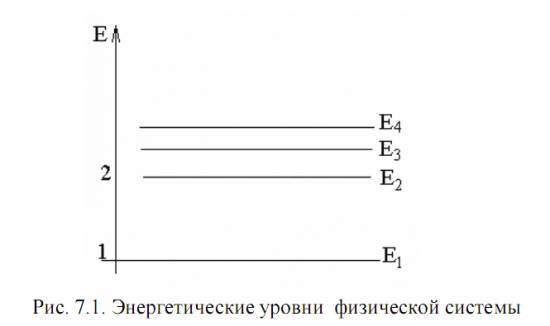
Каждому электрону в некоторой физической системе (например, в атоме или молекуле) соответствует свое состояние, т.е. своя энергия, причем эта энергия имеет дискретное значение. На рис. 7.1 приведена схема энергетических уровней такой физической системы (на примере атома) [1]. Обратимся к двум из уровней этой системы - 1 и 2. Уровень 1 соответствует основному состоянию физической системы, где нахождение ее наиболее вероятно. На уровень 2 система (электрон в атоме) может попасть, если ей передана некоторая энергия, равная hv = | E2 - E1|. Этот уровень 2 атома является возбужденным состоянием. Если система (атом) находится в состоянии 2 в течение времени t0, то существует конечная вероятность, что он перейдет в состояние 1, испустив при этом квант электромагнитной энергии hv = E2 - E1. Этот процесс, происходящий без воздействия внешнего поля случайно во времени (хаотически), называется спонтанным. Среднее число атомов, испытывающих спонтанный переход из состояния 2 в состояние 1 за одну секунду -dN2 / dt = A2 1 * N2 = N2 / ( tcn )2 1
(7.1) где А21 - скорость (вероятность) спонтанного перехода, ( tcn )21 = A21-1 называется временем жизни атома в возбужденном состоянии, связанным с переходом 2→1. Спонтанные переходы происходят из любого данного состояния только в состояния, лежащие по энергии ниже (например, если атом находится в состоянии 3, то возможны прямые переходы 3→2, 3→1, а попавший на уровень 2 атом переходит спонтанно на уровень 1). При наличии электромагнитного поля, имеющего частоту v ~ ( E2 - E1 ) / h атом может совершить переход из состоянии 1 в состояние 2, поглощая при этом квант электромагнитного поля (фотон) с энергией hv. Однако, если атом в тот момент, когда он подвергается действию электромагнитного поля, уже находится в состоянии 2, то он может перейти в состояние 1 с испусканием кванта с энергией hv под воздействием этого поля. Этот переход соответствует индуцированному излучению. Процесс индуцированного перехода от спонтанного отличает то, что для индуцированного перехода скорости переходов 2→1 и 1→2 равны, в то время как для спонтанного процесса скорость перехода 1→2, при котором энергия атома увеличивается, равна нулю. Кроме этого, индуцированные процессы имеют и другие принципиальные особенности:
Таким образом, можно утверждать, что вынуждающее и индуцированное (вынужденное) излучения оказываются строго когерентными. Рассмотрим случай, когда плоская монохроматическая волна с частотой v и интенсивностью Iv распространяется через среду с объемной плотностью атомов N2 на уровне 2 и N1 на уровне 1. Если ввести скорость переходов, которые индуцируются монохроматическим полем с частотой v, обозначив ее через Wi (v), то можно оценить условия, при которых будет существовать индуцированное излучение. За 1 с в объеме 1 м3 возникает N2Wi индуцированных переходов с уровня 2 на уровень 1 и N1Wi переходов с 1 на 2 уровень. Таким образом, полная мощность, генерируемая в единичном объеме P / V = ( N2 - N1 ) * Wi * hv (7.2) Это излучение когерентно суммируется с излучением бегущей волны с сохранением фазы, что при отсутствии рассеяния приводит к увеличению интенсивности на единицу длины. В результате dFy / dz = ( N2 - N1 ) * Wi * hv (7.3) Поскольку скорость индуцированного перехода прямо пропорциональна интенсивности [2]: Wi = G (v) * Iv (7.4) то из (7.3) следует, что Iv (z) - Iv (δ) eγ(v)z (7.5) γ (v) = ( N2 - N1 ) * G (v) (7.6) Следовательно, интенсивность волны экспоненционально нарастает, когда населенность уровня 2 (N2) превышает населенность первого уровня N1 (населенность инвертирована - обратна, N2>N1), или затухает, когда N2<N1. Первый случай соответствует лазерному излучению, а второй характерен для атомных систем при тепловом равновесии. Добавил: naddy (09.05.2010) | Категория: Квантовая физика Просмотров: 11721 | Загрузок: 1 | Рейтинг: 0.0/0 | Теги: |
| Комментарии (0) | |