Л/Р: Изучение выпрямляющего действия электронно-дырочного перехода

11.1 Цель работы

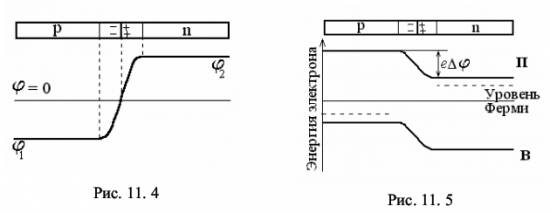
Изучение свойств p-n-перехода, снятие вольтамперной характеристики полупроводникового диода и экспериментальная проверка выпрямляющих свойств диода.

11.2 Содержание работы

Полупроводники – это широкий класс веществ, характеризующийся значениями удельной электропроводности, промежуточными между удельной электропроводностью металлов и хороших диэлектриков. Характерной особенностью полупроводников, отличающей их от металлов, является возрастание электропроводности с ростом температуры [1,2].

Типичными полупроводниками являются элементы IV группы периодической системы Менделеева – германий и кремний. Они образуют решетку типа алмаза, в которой каждый атом связан ковалентными (парно-электронными) связями с четырьмя равноотстоящими от него соседними атомами [2, 3]. Условно та-кое взаимное расположение атомов можно представить в виде плоской структуры, изображенной на рис. 11.1, а. Кружки со знаком «+» обозначают положительно заряженные атомные остатки (т.е. ту часть атома, которая остается после удаления валентных электронов), кружки сплошные – валентные электроны, двойные линии – ковалентные связи.

При нагревании ковалентные связи могут разрываться. Электрон, потерявший связь с атомом, становится свободным. Покинутое электроном место пере-стает быть нейтральным, в его окрестности возникает избыточный положительный заряд, т.е. образуется дырка (на рис. 11.1, а она изображена маленьким кружком). На это место может перескочить электрон одной из соседних пар. В результате дырка начинает так же странствовать по кристаллу, как и освободившийся электрон.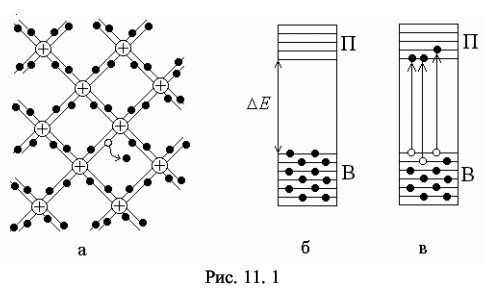



Когда внешнее электрическое поле отсутствует, электроны проводимости и дырки двигаются хаотически. При включении поля на хаотическое движение накладывается упорядоченное движение: электронов – против поля и дырок – в направлении поля, в результате происходит перенос заряда вдоль кристалла. Такая электропроводность полупроводников называется собственной (число электронов равно числу дырок).

С точки зрения зонной теории твердых тел у химически чистых полупроводников при абсолютном нуле все уровни валентной зоны В (рис. 11.1, б) полностью заполнены электронами, а в зоне проводимости П электроны отсутствуют. Валентная зона В отделена от зоны проводимости запрещенной зоной. Ширина запрещенной зоны ∆Е у полупроводников с собственной проводимостью не более 1 эВ [3], тем не менее электрическое поле не может перебросить электроны из валентной зоны в зону проводимости, поэтому при абсолютном нуле такие полу-проводники ведут себя как идеальные диэлектрики.

При нагревании или облучении полупроводника электронам верхних уровней валентной зоны сообщается дополнительная энергия – энергия активации ∆Е, и они могут переходить на нижние уровни зоны проводимости (рис. 11.1, в). При этом в валентной зоне освобождаются энергетические уровни – образуются дырки. При наложении внешнего электрического поля электроны зоны проводимости переводятся на более высокие, а дырки валентной зоны на более низкие энергетические уровни. Электропроводность полупроводника становится отличной от нуля.

Наибольшее техническое применение находят полупроводники с примесной проводимостью. Примесная проводимость возникает, если некоторые атомы полупроводника заменить в узлах кристаллической решетки атомами, валентность которых отличается на единицу от валентности основных атомов.

На 11.2(а) условно изображена решетка германия с примесью пятивалентных атомов фосфора.

Для образования ковалентной связи с соседями атому фосфора недостаточно четырех электронов. Следовательно, пятый валентный электрон связан только со своим атомом. Энергия активации такого электрона ∆E_g невелика (∆E_g ~ 0,01 эВ). При небольшом повышении температуры электрон отщепляется от атома и становится свободным. Эти электроны и обуславливают перенос заря-да при наложении внешнего электрического поля. Это полупроводник с электронной проводимостью (полупроводник n-типа).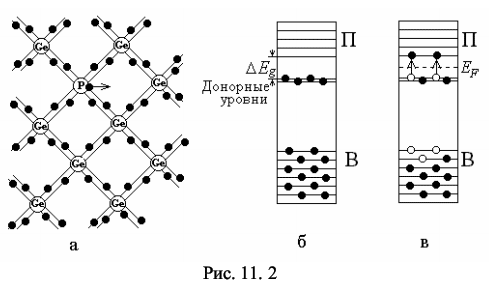



В отличие от собственной проводимости образование свободного электрона в полупроводнике n-типа не сопровождается нарушением ковалентных связей, т.е. образованием дырки, хотя в окрестности атома примеси возникает избыточный положительный заряд, но он связан с этим атомом и перемещаться по решетке не может [2, 3].

С точки зрения зонной теории внедрение в решетку атомов с большей валентностью соответствует появлению локальных донорных уровней, которые располагаются вблизи дна зоны проводимости (см. рис. 11.2, б). Поскольку ∆Eg < ∆E, то уже при небольшом повышении температуры электроны с донорных уровней начнут переходить в зону проводимости (см. рис. 11.2, в), так что при комнатной температуре они практически все будут находиться в зоне проводимости.

Если валентность атома на единицу меньше валентности основных атомов, то одна из ковалентных связей окажется неукомплектованной и будет представлять собой место, способное захватить электрон (см. рис. 11.3, а). При переходе на это место электроны одной из соседних пар возникает дырка, которая будет кочевать по кристаллу. Это полупроводник с дырочной проводимостью (полупроводник p-типа).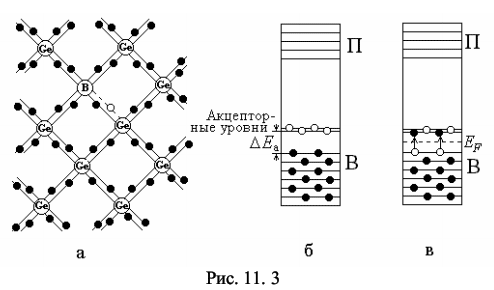



С точки зрения зонной теории внедрение в решетку атома с меньшей валентностью соответствует появлению локальных акцепторных уровней, расположенных вблизи потолка валентной зоны (см. рис. 11.3, б), в валентной зоне появляются дырки. Таким образом, примесная проводимость обусловлена электрона-ми в случае донорной примеси и дырками в случае акцепторной. Эти носители являются основными. Кроме них полупроводник содержит неосновные носители: электронный полупроводник – дырки, дырочный полупроводник – электроны. Концентрация их значительно ниже концентрации основных носителей.



Если в одну часть полупроводника ввести акцепторную примесь, а в другую – донорную, то первая часть будет иметь дырочную (p-типа), а вторая – электронную (n-типа) проводимость. Тонкий слой на границе между этими полупроводниками с разным типом примесной проводимости, называется электронно-дырочным переходом или просто p-n-переходом.

Диффузия основных носителей из p-области в n-область и наоборот приводит к рекомбинации (т.е. нейтрализации) электронов и дырок, вследствие чего по-граничный слой оказывается сильно обедненным носителями тока и, следовательно, приобретает большое сопротивление. Протяженность этого слоя ~ 10–5 -10^–6см, т.е. намного превышает размеры атомов [5]. Одновременно в граничном слое n-полупроводника, потерявшем часть своих электронов, образуется объемный положительный заряд ионизированных донорных атомов: в граничном слое p-полупроводника, получившем эти электроны, образуется объемный отрицательный заряд неподвижных атомов акцепторной примеси. Между этими слоями возникает контактная разность потенциалов ∆φ = φ2 – φ1, препятствующая дальнейшей диффузии основных носителей (рис. 11.4).

С точки зрения зонной теории основные носители диффундируют до тех пор, пока не произойдет выравнивание уровней Ферми E_F, расположенных соответственно в нижней и верхней половинах запрещенных зон у акцепторного (см. рис. 11.3, в) и донорного (см. рис. 11.2, в) полупроводников. Энергетические зоны при этом изгибаются (см. рис. 11.5), образуя потенциальный барьер e∆φ для основных носителей.

Изгибание энергетических зон вызвано тем, что потенциал p-области в со-стоянии равновесия ниже, чем потенциал n-области (см. рис. 11.4), соответствен-но потенциальная энергия электрона E_э в р-области выше, чем в n-области (см. рис. 11.5 и сплошную кривую на рис. 11.6, а). Заряд дырок противоположен заряду электрона, поэтому их потенциальная энергия E_д больше там, где меньше E_э (см. рис. 11.6, а).

В состоянии равновесия некоторому количеству основных носителей удается преодолеть потенциальный барьер, вследствие чего через переход течет небольшой ток I_осн. Этот ток компенсируется встречным током носителей неосновных носителей I_неосн. Неосновных носителей очень мало, но они легко «скатываются» с потенциального уступа. Равновесие устанавливается при такой высоте потенциального барьера, при которой оба тока компенсируют друг друга.

Сопротивление p-n-перехода резко меняется при приложении к нему внеш-него электрического поля. Если к p-n-переходу приложить напряжение U_ист от внешнего источника тока таким образом, чтобы p-область заряжалась положительно относительно n-области (рис. 11.6, б), то высота потенциального барьера (и его ширина ∆x) уменьшится на eU_ист. Это приведет к увеличению силы тока основных носителей I_осн. Ток же неосновных носителей от высоты потенциального барьера не зависит и следовательно не изменится. В результате через контакт идет ток (Iо_сн – I_неосн), направленный от p к n. Причем сила тока с увеличением напряжения экспоненциально возрастает. Такое направление поля (и тока) называется прямым или проводящим.

Если же к p-n-переходу приложить внешнее напряжение, как показано на рис. 11.6, в, то высота потенциального барьера (и его ширина) увеличится, сопротивление контактного слоя резко возрастает. Сила тока I_осн уменьшится при этом практически до нуля, так что через контакт будет течь лишь ток неосновных носителей. Такое направление поля (и тока) называется обратным, или запирающим.

Таким образом, элемент, содержащий p-n-переход, обладает односторонней проводимостью и называется полупроводниковым диодом. Прикладывая к такому элементу переменное по знаку напряжение, получают ток только одного направления.

Изучению свойств p-n-перехода и посвящена данная работа, которая состоит из двух частей. В первой части работы строится и анализируется вольтамперная характеристика (зависимость силы тока от напряжения) полупроводникового диода. Во второй части изучается применение диодов для выпрямления переменного тока.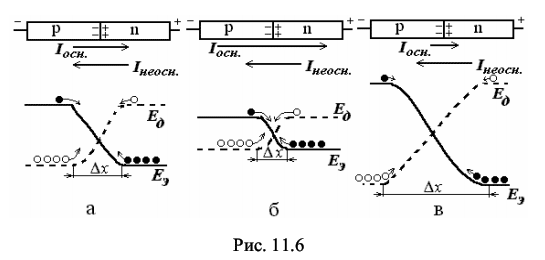



11.3. Описание лабораторной установки

Для получения вольтамперной характеристики диод включается в электрическую цепь, принципиальная схема которой приведена на рис. 11.7.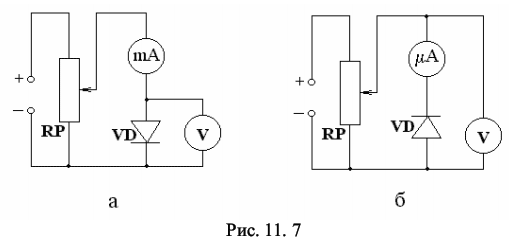



От стабилизирующего источника питания напряжение подается на диод VD. Схема 11.7, а относится к измерениям в прямом направлении, а схема 11.7, б – в обратном. Переход от одной схемы к другой осуществляется с помощью пере-ключателя SA, который на рисунке 11.7 не изображен. Напряжение в обоих слу-чаях регулируется потенциометром RP и измеряется вольтметром V. При прямом направлении тока в цепь включается миллиамперметр μA (рис. 11.7, а), при об-ратном – микроамперметр µА (рис.11.7, б). Для этих измерений используются амперметры, рассчитанные на измерение токов до 100 мА в прямом и до 100 мкА -в обратном направлениях. Измеряемое напряжение не превышает 10 В. Подключение соответствующих шунтов и дополнительных сопротивлений в каждом исследовании осуществляется автоматически.

Выпрямляющее действие диода изучается по схеме, приведенной на рис. 11.8.

Переменное напряжение с вторичной обмотки трансформатора блока питания подается на диод или систему диодов, соединенных по схеме моста или непосредственно прикладывается к резистору R (рис. 11.8).

Форма и амплитуда этого напряжения регистрируется осциллографом.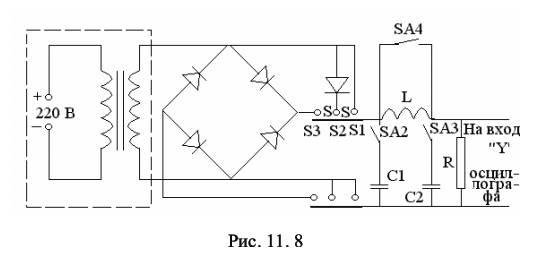


Включение диода или систем диодов осуществляется переключателем S. (Положение S1 переключателя соответствует подача напряжения непосредственно на резистор, S2 – подача напряжения на резистор с диода, S3 – подача напряжения на резистор с системы диодов, соединенных по схеме моста).

Конденсаторы С1 и С2, а так же дроссель L образуют электрический фильтр. Включение их осуществляется соответственно тумблерами SA2, SA3, SA4.

В работе электрические цепи, схемы которых приведены на рис. 11.7 и 11.8, собраны соответственно в верхней и нижней части корпуса лабораторной установки. Переход от одной схемы к другой осуществляется с помощью тумблера SA1, который на рисунках не указан. Все ручки управления и шкалы приборов расположены на лицевой панели установки.


11.4. Методика проведения эксперимента и обработка результатов
11.4.1. Методика эксперимента

Подавая на диод VD напряжение (см. рис. 11.7) и плавно меняя его потенциометром RP, измеряют силу тока при различных значениях приложенного прямого, а затем обратного напряжений. По полученным значениям строят график вольтамперной характеристики.

Так как сопротивление p-n-перехода гораздо больше сопротивления остальной части цепи, то падение напряжения внешнего поля происходит в основном на p-n-переходе [4]. Это обстоятельство позволяет рассчитать сопротивление p-n-перехода при различных значениях прямого и обратного напряжений и построить соответствующие графики зависимостей сопротивления от напряжения.

Поскольку вольтамперная характеристика нелинейна, то сопротивление рассчитывается по формуле




где ∆U и ∆I – соответственно разности между двумя ближайшими измеренными значениями напряжений и силы токов.

В электрической цепи, схема которой приведена на рис. 11.8, диод работает как выпрямитель и преобразует переменный ток в пульсирующий. Причем, если в цепь включается один диод, то происходит однополупериодное выпрямление, а если диоды включаются по схеме моста, то двухполупериодное.

Введение в электрическую цепь конденсаторов С1 и С2 приводит соответственно к уменьшению выпрямленного тока при зарядке конденсаторов и к увеличению тока при разрядке, т.е. к сглаживанию пульсаций. Дроссельная катушка L также сглаживает пульсации переменной составляющей общего тока. Соответствующие осциллограммы наблюдаются на экране осциллографа.


11.4.2. Порядок выполнения работы
11.4.2.1. Снятие вольтамперной характеристики

1. Найдите на лицевой панели установки все элементы электрических схем, изображенных на рис. 11.7 и 11.8.
2. Включите электрическую цепь, схема которой изображена на рис. 11.7, а, для чего тумблер SA1 поставьте в верхнее положение, а тумблер SA в положение «прямое». При этом вольтметр работает в диапазоне 0 – 10 В, а миллиамперметр – в диапазоне 0 – 100 мА.
3. Определите цену деления измерительных приборов и запишите в табл. 11.1.
4. Уменьшите сопротивление потенциометра RP до нуля.
5. Подайте напряжение на вход прибора.
6. С помощью потенциометра RP плавно увеличивайте напряжение и вначале через каждое деление, а затем через 2-3 деления вольтметра измеряйте силу тока. Результаты 13-15 измерений занесите в таблицу 11.2.
7. Тумблер SA поставьте в положение «обратное». При этом микроамперметр работает в диапазоне 0-100 мкА, вольтметр – в диапазоне 0-10 В.
8. Определите цену деления микроамперметра и вольтметра и запишите в табл. 11.1.
9. Повторите задание пп. 4 и 6. Результаты измерений запишите в табл. 11.3.

11.4.2.2. Проверка выпрямляющих свойств диода

1. Подготовьте осциллограф к работе в соответствии с указаниями на лабораторном столе.
2. Переключите тумблер SA1 в нижнее положение.
3. Переключатель S переведите в положение S1.
4. Включите осциллограф и получите на экране осциллограмму переменного напряжения. Ручками «частота плавно» и «синхронизация» остановите изображе-ние сигнала. Расположите его симметрично относительно горизонтальной оси времени (амплитуда сигнала при этом должна быть не менее 25-30 мм) и зарисуй-те осциллограмму.
5. Введите в цепь диод, для чего переключатель S переведите в положение S2. При этом на экране осциллографа будет наблюдаться синусоида со срезанными отрицательными (нижними) полупериодами.
6. Зарисуйте преобразованный сигнал, предварительно расположив его таким образом, чтобы значение первоначальной амплитуды сохранилось.
7. Введите в цепь мостик диодов, для чего переключатель переведите в положение S3. Зарисуйте осциллограмму двухполупериодного выпрямления.
8. Введите в цепь конденсатор C1, включив тумблер SA2 (см. рис. 11.8), и за-рисуйте осциллограмму.
9. Введите в цепь дополнительно конденсатор С2, включив тумблер SA3 (см. рис. 11.8), и зарисуйте осциллограмму.
10. Введите в цепь катушку индуктивности, поставьте тумблер SA4 в нижнее положение (в схеме, изображенной на рис. 11.8, это соответствует размыканию ключа, поставленного параллельно катушке индуктивности). Полученную диаграмму зарисуйте.
11. Закончив работу, обесточьте установку.

11.4.3. Обработка результатов измерений

1. Постройте по данным табл. 11.2 и 11.3 график зависимости I = ƒ(U). При по-строении графика силу тока и напряжение следует откладывать на одной координатной сетке, считая прямой ток и напряжение положительными, а обратный ток и напряжение – отрицательными (масштаб для силы тока в прямом и обратном направлениях возьмите разный).
2. Проанализируйте характер зависимости I = ƒ(U) и сделайте вывод, справедлив ли закон Ома для системы, содержащий p-n-переход.
3. Определите ∆U и ∆I – разность между последующим и предыдущим значениями напряжений и токов и запишите в соответствующие столбцы таб. 11.2 и 11.3.
4. Рассчитайте сопротивление диода по формуле 11.1 и запишите в табл. 11.2 и 11.3.
5. Постройте график зависимости R = ƒ(U) для прямого и обратного напряже-ний и проанализируйте эти зависимости.

11.5. Перечень контрольных вопросов

1. Объясните механизм собственной и примесной проводимости в полупроводниках с точки зрения теории твердого тела.
2. Что является «основными» и «неосновными» носителями тока в полупроводниках n- и p-типа?
3. Объясните механизм образования контактной разности потенциалов в полупроводниках с точки зрения зонной теории твердого тела.
4. Объясните, как изменяется высота потенциального барьера при приложении внешнего прямого и обратного напряжений.
5. Как работает одно- и двухполупериодный выпрямитель?
6. Объясните принцип работы электрических фильтров.

1. Физический энциклопедический словарь. М.: Советская энциклопедия, 1983. – 928 с.
2. Савельев И. В. Курс общей физики. т. 3. М.: Наука, 1982.- § 57 – 59, 64.
3. Детлаф А. А., Яворский Б. М. Курс физики. М.: Высшая школа, 1977. – § 43.4, 44.3, 44.4.
4. Епифанов Г. И. Физика твердого тела. М.: Высшая школа, 1977. – § 42-46, 56, 57, 76.
5. Лабораторные занятия по физике. /Под ред. Л. Л. Гольдина. М.: Наука, 1983. – 704 с.