Сидят два студента с ФИЗТЕХА в столовой и бурно обсуждают какую-то задачу. Мимо них проходит весьма эффектная девушка. Они одновременно замолкают и провожают её взглядом... После паузы один говорит:
Построение математических моделей методом регрессионного анализа
[
]
01.07.2010, 00:00
Регрессионный анализ – это наиболее известный метод построения модели идентификации. Он основан на двух предположениях:
метод применим только к математическим моделям линейным по идентифицируемым параметрам;
в качестве меры рассогласования математической модели с экспериментальными данными берется сумма квадратов отклонений расчетных и экспериментальных значений выходной величины.
Метод регрессионного анализа включает следующие этапы
Минимизация функции ошибки. Для этого все частные производные функции ошибки по всем параметрам приравниваются к нулю.
Решение полученной системы линейных уравнений дает искомые значения параметров.
Идентификация линейной функции
Постановка задачи:
Решить задачу параметрической идентификации и найти параметры a0, a1, a2 математической модели, имеющей следующую структуру: y = a0 + a1x1 + a2x2 ; для наилучшего описания следующих экспериментальных данных.
Входные воздействия
x1
1
0
1
2
x2
1
1
0
1
Выходное воздействие
y
-1
-3
3
1
Решение:
1. Составим сумму квадратов отклонений (функцию ошибки):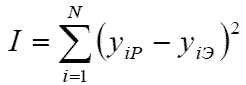
где N = 4 – количество экспериментов, yiР – расчетное значение выходного воздействия, yiЭ – экспериментальное значение выходного воздействия (из таблицы).
2. Минимизируем полученную функцию ошибки:
I( a0, a1, a2 ) -> min
3. Применим необходимое условие существования экстремума (минимума) функции многих переменных.
Если непрерывная дифференцируемая функция имеет в некоторой точке экстремум, то ее градиент (вектор частных производных) равен нулю.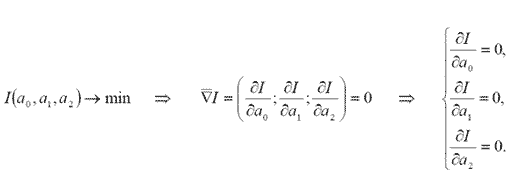
4. Вычислим частные производные функции ошибки и приравняем их к нулю:
5. Решим полученную систему линейных уравнений и находим три коэффициента "a".
Система решается достаточно просто, поэтому не будем расписывать её решение подробно. А ответ таков: a0 = 1, a1 = 2, a0 = -4, то-есть полученная модель выглядит следующим образом: y = 1 + 2*x1 - 4*x2.
