Изучение температурной зависимости электропроводности металлов и полупроводников

Цель работы

Исследование зависимости электрического сопротивления металлических проводников и полупроводников от температуры; расчет температурного коэффициента сопротивления а и определение ширины запрещенной зоны полупроводника ΔE.

10.3. Описание лабораторной установки

В данной работе для измерения электрических сопротивлений металлического проводника и полупроводника при различных температурах используется установка, электрическая схема которой приведена на рис. 10.4.

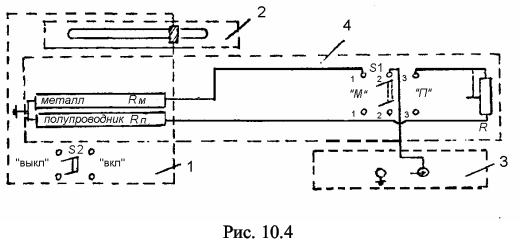
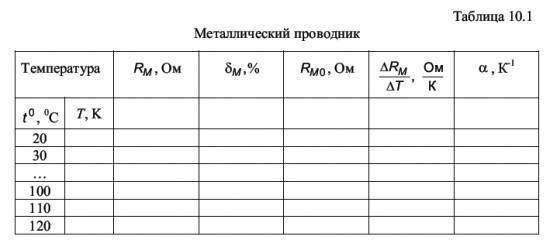
Функционально установка может быть разбита на четыре блока. Б л о к 1 служит для нагревания исследуемых образцов. Он представляет собой нагрева-тельную печь, включаемую тумблером S2. Б л о к 2 – жидкостный термометр – служит для измерения температуры образцов. Б л о к 3 – цифровой универсальный вольтметр, работающий в режиме измерения сопротивлений. Б л о к 4 – представляет собой комплект исследуемых образцов: металл R_М и полупроводник R_П. Выбор металлического проводника или полупроводника осуществляется тумблером S1: положение "М" соответствует металлическому образцу, положение "П" – полупроводнику.

Используемые образцы размещены внутри нагревательной печи; панель с тумблером S1 расположена справа на боковой стороне нагревательной печи.

10.4. Методика проведения эксперимента и обработка результатов

10.4.1. Методика эксперимента

В основе настоящей работы лежат прямые измерения электрических сопротивлений и температур методом непосредственного отсчета с цифрового табло вольтметра и со шкалы термометра соответственно.

Электрическое сопротивление химически чистых металлов большом интервале температур растет прямо пропорционально температуре:

(10.11)

где ΔR = R_М - R_М0, ΔT = T - T₀.

Построив график зависимости R_M = ƒ(T), (R_M - откладываем по оси ординат, T - по оси абсцисс, (рис. 10.5), можно определить величины R_M0 и α.

Из рис. 10.5 видно, что отношение

ΔR_М / ΔT = (R_М - R_М0 ) / (T -T₀ ) = (R_М2 - R_М1 ) / (T₂ -T₁ )

(10.11)

представляет собой угловой коэффициент линейной зависимости R_M = ƒ(T).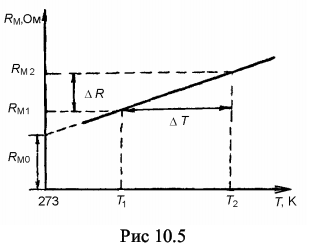

Определив по графику R_M0 и угловой коэффициент линейной зависимости ΔR_М / ΔT, по формуле (10.11) можно рассчитать температурный коэффициент сопротивления α.

Сопротивление полупроводников   в широком интервале температур экспоненциально убывает с ростом температуры:

Rп = R_П0 · exp (ΔE / 2kT)

(10.13)

где R_П0 - сопротивление полупроводника при T →∞;
ΔE - ширина запрещенной зоны.

Логарифмирование выражения (10.13) дает

ln (R_П / R_П0) = ΔE / 2kT

ln R_П1 - ln R_П2 = (ΔE / 2k) · ((1 / T₁) - (1 / T₂))

(10.17)

Или

Δln (R_П ) = (ΔE / 2k) · Δ(1 / T)

(10.18)

Откуда

ΔE =  2k · (Δln (R_П ) / Δ(1 / T))

(10.19)

Отношение Δln (R_П ) = Δ(1 / T) представляет собой угловой коэффициент линейной зависимости ln R_П  = ƒ (1 / T) (рис.10.6).

Определив   по   графику   угловой   коэффициент   линейной   зависимости Δln (R_П ) = Δ(1 / T), можно по формуле (10.19) рассчитать ширину запрещенной зоны ΔE.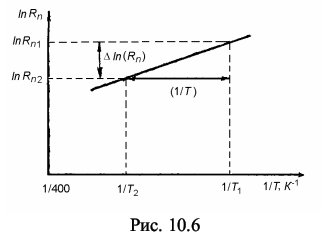

10.4.2. Порядок выполнения работы

1. Подготовьте цифровой вольтметр к работе так, как рекомендуется в инструкции по эксплуатации, помещенной на лабораторном столе.
2. Вставьте вилки сетевых шнуров нагревательной печи и универсального цифрового вольтметра в сетевые розетки.
3. По термометру нагревательной печи определите начальную температуру образцов металла и полупроводника; результаты всех измерений записывайте в табл. 10.1 и 10.2.
4. Включите цифровой вольтметр в сеть и прогрейте его в течение времени, указанном в инструкции по эксплуатации.
5. При начальной температуре измерьте сопротивление металла (тум-блер) S1 - положение "М") и полупроводника (тумблер S1 - в положение "П").
6. Тумблером S2, расположенным на лицевой панели нагревательной печи, включите печь в сеть; при этом должна загореться сигнальная лампочка.
7. Произведите измерения электрических сопротивлений металла и полупроводника в интервале температур 293-393 К через 10 К (10⁰С).
8. Закончив измерения, выключите вольтметр и печь, откройте дверцу печи для быстрейшего остывания образцов.
   

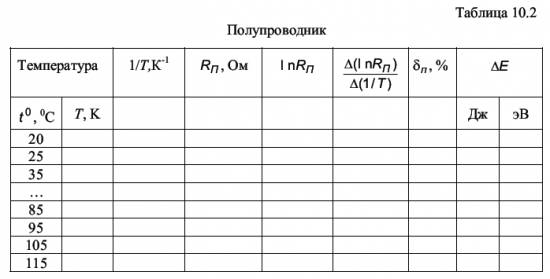
10.4.3. Обработка результатов измерения

1. Постройте на миллиметровой бумаге график зависимости сопротивления металлического проводника от температуры Т. Точка пересечения координатных осей по оси абсцисс 273 К.
2. Продолжив график R_M = ƒ(T) до пересечения с осью ординат, определите значение R_M0.
3. По графику (см. рис. 10.5) в соответствии с формулой (10.12) определите
   угловой коэффициент ΔR / ΔT и по формуле (10.11) рассчитайте температурный коэффициент сопротивления α - исследуемого образца металла.
4. Для полупроводника рассчитайте значения lnR_П и 1 / Т.
5. Постройте на миллиметровой бумаге график зависимости логарифма сопротивления полупроводника lnRП от обратной температуры 1/Т. Точка пересечения координатных осей соответствует по оси абсцисс   1 K-1.
   400
6. По графику зависимости lnR_П = ƒ(1 / T) (см. рис. 10.6) определите угловой коэффициент Δ(lnR_П) /Δ(1/T) и рассчитайте по формуле (10.19) ширину запрещенной зоны ΔE исследуемого полупроводника.
7. В соответствии с формулой, указанной в инструкции по эксплуатации вольтметра (на лабораторном столе), рассчитайте относительные погрешности измерений сопротивлений металлического проводника δ_M и полупроводника δ_П.
   

10.5. Перечень контрольных вопросов

1. Что представляют собой проводники и полупроводники с точки зрения зонной теории?
2. Что такое электропроводность (сопротивление), какова ее (его) количественная характеристика? (Классические и квантово-механические представления).
3. Как зависит электропроводность (сопротивление) металлов и полупроводников от температуры? Объясните различие в изменении их электропроводности в зависимости от температуры.
4. Объясните собственную и примесную проводимость полупроводников. Как влияет на электропроводность полупроводника различная степень его легирования?
5. Какова сущность электрон-примесного и электрон-фононного рассеяния?
6. Объясните сущность правила Матиссена.
7. Выведите формулу, используемую в работе, для определения температурного коэффициента сопротивления металлов.
8. Выведите формулу для определения ширины запрещенной зоны полупроводника.
   

СПИСОК  РЕКОМЕНДУЕМОЙ  ЛИТЕРАТУРЫ

1. Савельев И.В., Курс общей физики. В 3-х т. -М.: Наука, 1982. Т.2. С. 104-106, 229-231; Т.3. С. 192-206.
   
2. Детлаф А.А., Яворский Б.М. Курс физики. -М.: Высшая школа, 1989. С. 195-202, 501-504, 512-523.
3. Трофимова Т.И. Курс физики. -М.: Высшая школа, 1994. С. 436-438, 439-441, 443-451.