Презентация на тему "Движение. и его виды" по геометрии

Презентация на тему "Движение. Виды движения" по геометрии в формате powerpoint. В данной презентации для учеников средней школы дается определение движения и рассмотрены различные его виды.

Фрагменты из презентации

Движение плоскости – это отображение плоскости на себя, сохраняющее расстояния.

Виды движения:

1. Симметрия:
• осевая,
• центральная,
• скользящая.
• зеркальная.
2. Параллельный перенос.
3. Поворот.

История симметрии

• Однако как люди дошли до такой сложной и одновременно такой простой вещи, как симметрия?
• Ещё древние греки считали, что симметрия – это гармония, соразмерность. Они же и ввели термин συμμετρία, который сейчас перешёл в русское слово «симметрия»
• А у древних народов, таких как шумеры и египтяне, у первобытных племён, да и у кое-кого в наше время симметрия ассоциируется не только с красотой и гармонией, но и прежде всего с магией. Не зря же люди в эпоху мегалита для ритуальных целей сооружали кромлихи в форме круга – «идеально симметричной» геометрической фигуры.

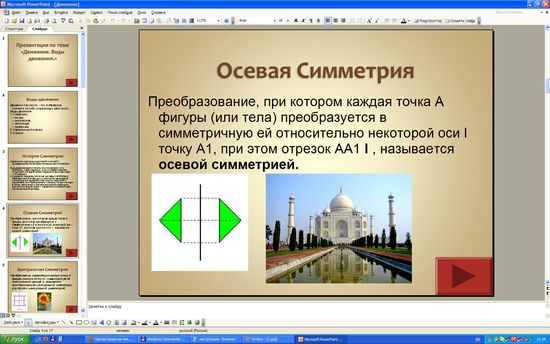
Осевая симметрия

Преобразование, при котором каждая точка А фигуры (или тела) преобразуется в симметричную ей относительно некоторой оси l точку А1, при этом отрезок АА1 l , называется осевой симметрией.

Центральная симметрия

Преобразование, переводящее каждую точку А фигуры (тела) в точку А1, симметричную ей относительно центра О, называется преобразованием центральной симметрии или просто центральной симметрией.

Скользящая симметрия

Скользящей симметрией называется такое преобразование, при котором последовательно выполняются осевая симметрия и параллельный перенос.

Зеркальная симметрия

Если преобразование симметрии относительно плоскости переводит фигуру (тело) в себя, то фигура называется симметричной относительно плоскости, а данная плоскость – плоскостью симметрии этой фигуры.

Роль симметрии в мире

А собственно, как бы нам жилось без симметрии? Точнее, какую роль играет симметрия в нашем мире? Неужели она лишь украшает его? Оказывается, что без симметрии наш мир выглядел бы совсем по-другому. Ведь это именно на симметрии основаны многие законы сохранения. Например, законы сохранения энергии, импульса и момента импульса являются следствиями пространственно-временных симметрий, которые являются, как математическими, так и физическими симметриями. И без этих симметрий не было бы законов сохранений, которые во многом управляют нашим миром. Так что симметрия – пожалуй, чуть ли не самая главная вещь во Вселенной.

Параллельный перенос

Параллельный перенос ― частный случай движения, при котором все точки пространства перемещаются в одном и том же направлении на одно и то же расстояние. Иначе, если M ― первоначальное, а M' ― смещенное положение точки, то вектор M’   ― один и тот же для всех пар точек, соответствующих друг другу в данном преобразовании.a

Поворот

Поворот — частный случай движения, при котором по крайней мере одна точка плоскости (пространства) остаётся неподвижной. При вращении плоскости неподвижная точка называется центром вращения, при вращении пространства неподвижная прямая называется осью вращения. Вращение плоскости (пространства) называется собственным (вращение первого рода) или несобственным (вращение второго рода) в зависимости от того, сохраняет оно или нет ориентацию плоскости (пространства).

Вывод

Движение и все его виды очень важны в нашей жизни. Без них не было бы тех архитектурных сооружений и технических достижений, что мы имеем.