Главная Квантовая физика » Файлы » Методика выполнения лабораторных работ по физике » Квантовая физика [ Добавить материал ]

Изучение спектра испускания водорода

Цель работы

Исследовать спектр испускания атомов водорода в видимой области. Экспериментально определить постоянную Ридберга и массу электрона.

Для начала рекомендуется изучить теорию Водородоподобных атомов в классической механике.


4.2.4. «Водородоподобные атомы» в квантовой механике

Значения энергии атома En получают при решении стационарного уравнения Шрёдингера для движения электрона в кулоновском поле ядра с зарядом Ze:

▼2Ψ + (2·me / ђ2) * ( E + (1 / 4·π·ε0) * (Z·e2 / r) ) = 0
(4.17)
где ▼2 - оператор Лапласа, ▼2 = (∂2 / ∂x2) + (∂2 / ∂y2) + (∂2 / ∂z2).

Волновая функция Ψ (пси-функция) характеризует состояние микрочастицы.

Квадрат модуля волновой функции даёт плотность вероятности (вероятность, отнесённую к единице объёма) нахождения частицы в соответствующем месте пространства:

|Ψ|2  = dP / dV
(4.18)
где dP - вероятность того, что частица будет обнаружена в пределах объёма dV.

По квантовой теории боровские орбиты электрона представляют собой геометрическое место точек, в которых с наибольшей вероятностью может быть обнаружен электрон.

По теории Бора вероятность обнаружить электрон в состоянии с n = 1 отлична от нуля для r = a0.

Согласно же квантовой механике, эта вероятность лишь достигает максимума при r = a0, но она отлична от нуля во всём пространстве. На рис. 4.3 сопоставлены вероятности обнаружить электрон на различных расстояниях от ядра по теории Бора и по квантовой механике.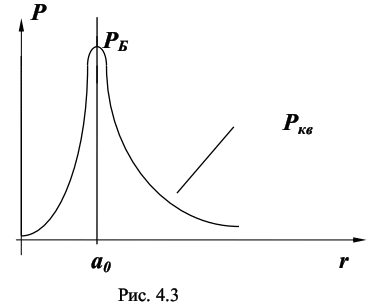



Уравнение (4.17) имеет решения в следующих случаях:
  1. при любых положительных энергиях Е;
  2. при дискретных отрицательных значениях энергии, равных

En = - (me·Z2·e4 / 8·ε02·n2·h) (n =1, 2, 3, ...)
(4.19)

  • Случай Е > 0 соответствует свободному электрону, пролетающему вблизи ядра и удаляющемуся снова на бесконечность.
  • Случай Е < 0 соответствует электрону, связанному с ядром.

Значения энергии (4.19) называются собственными, волновые функции Ψ, соответствующие этим значениям энергии, также называются собственными.

Сравнение с выражением (4.11) показывает, что квантовая механика приводит к таким же значениям энергии водородного атома, какие получались в теории Бора. Однако в квантовой механике эти значения получаются как следствие основных положений этой науки. Бору же для получения такого результата пришлось вводить дополнительные предположения (постулаты).

Следует также отметить, что с возрастанием n соседние уровни энергии атома сближаются, и при n → ∞ расстояние между ними стремится к нулю, дискретность энергетического спектра становится всё менее заметной. Поэтому можно ожидать, что в таком случае квантовая система будет вести себя как классическая. Это положение было сформулировано Бором и названо им принципом соответствия.

В соответствии с этим принципом для очень больших круговых орбит электрона, т.е. когда n → ∞, полная энергия электрона становится непрерывной величиной. Принцип соответствия также позволяет объяснить сходство выражений для энергии, полученных классическим и квантово-механическим способом.

Из квантовой механики следует, что собственные функции Ψ уравнения Шрёдингера для атома водорода содержат три целочисленных параметра: n, l, m. Каждое Ψn, l, m определяет одно квантовое состояние.

Параметр n называется главным квантовым числом и определяет энергию атома; l - орбитальное квантовое число, определяет момент импульса атома; m - магнитное квантовое число, определяет проекцию момента импульса на некоторое выбранное направление. Эти квантовые числа связаны следующими соотношениями: при заданном главном квантовом числе n орбитальное квантовое число может иметь одно из следующих значений l = 0, 1, 2, ... n-1, т.е. всего n значений. При данном l магнитное квантовое число может принимать значения: m = -l, -(l - 1), ... , -1, 0, +1, ..., (l - 1), l, т.е. всего (2l + 1) различных значений. Таким образом, число возможных различных состояний водородоподобного атома, соответствующих определённому значению n, равно

∑ (2·l - 1) = n2
(4.20)
(сумма от l = 0 до n -1)

Поскольку энергия водородного атома не зависит от квантового числа l, все эти состояния имеют одинаковую энергию, если определённому уровню энергии соответствует больше, чем одно состояние, говорят, что уровень вырожден. Следовательно, уровни водородоподобного атома имеют вырождение кратности n2.

Для различных значений орбитального квантового числа l используются буквенные обозначения:

  •     состояние электрона с l = 0 обозначается s-состоянием;
  •     состояние электрона с l = 1 - р-состоянием;
  •     состояние электрона с l = 2 - d-состоянием; l = 3 - f-состоянием.

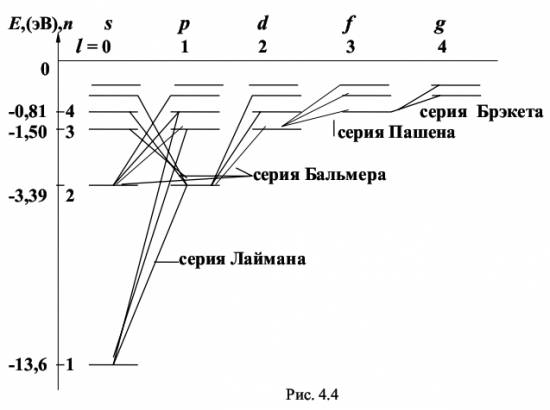
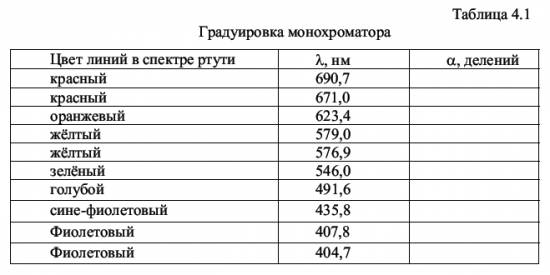
Значение главного квантового числа указывается перед условным обозначением состояния электрона, например, состояние электрона с n = 3 и l = 1 обозначается символом 3р.

В квантовой механике доказано и экспериментально подтверждено, что для орбитального квантового числа l существует правило отбора:

∆ l = ± 1
 (4.21)

Это означает, что возможны только такие переходы с излучением, при которых l изменяется на единицу.

В соответствии с изложенным возможные энергетические состояния и излучательные переходы атома водорода могут быть представлены схемой, показанной на рис. 4.4.

Пользуясь условными обозначениями состояний электрона, переходы, приводящие к возникновению серии Лаймана, можно записать в виде:

n·p → 1·s (n = 2, 3, ...);

серии Бальмера соответствуют переходы

n·p → 2·s, n·s → 2·p, n·d → 2·p (n = 3, 4, ..).



В настоящей работе изучается видимая область серии Бальмера, первые три линии которой имеют длины волн, соответствующие красному, сине-зелёному и сине-фиолетовому цвету. Определяя экспериментально длины волн в спектре водорода, вычисляют по формуле (4.2) постоянную Ридберга R, а по формуле (4.14) - массу электрона.

4.3. Описание лабораторной установки

Установка для наблюдения спектра состоит из источника света, конденсора и монохроматора УМ-2, который в данной работе используется как спектроскоп. Источниками света являются ртутная лампа и водородная трубка, возбуждение атомов в которых происходит с помощью газового разряда, возникающего при высоком напряжении. Для питания ртутной лампы служит блок питания, подключаемый к сети. Высоковольтное напряжение на водородную трубку подается со вторичной обмотки катушки Румкорфа, работающей в режиме повышающего трансформатора.

Оптическая схема монохроматора УМ-2, описание его работы и внешний вид установки приведены в описании лабораторной работы № 3 (см. настоящий сборник).

4.4. Методика проведения эксперимента и обработка результатов измерения
4.4.1. Методика эксперимента

Чтобы использовать монохроматор для изучения спектров, необходимо его проградуировать, т.е. поставить в соответствие делениям α на барабане длины волн эталонных спектральных линий. В качестве эталонного спектра в работе используется спектр ртути, состоящий из большого числа ярких линий, длины волн которых известны.

На основании полученных для спектра ртути данных строят градуировочный график. По этому графику определяются длины волн трёх линий в спектре водорода по значениям угла α шкалы барабана, соответствующих положению каждой из этих линий.

4.4.2. Порядок выполнения работы

  • 1)  Включите ртутную лампу с помощью тумблеров "сеть”, "лампа ДРШ” и последующего нажатия кнопки "пуск” на блоке питания.
  • 2)  Вращая барабан монохроматора, и наблюдая через окуляр зрительной трубы спектрокопа, отождествите наблюдаемый спектр с участком спектра ртути, изображенным на рисунке на лабораторном столе. При вращении барабана необходимо следить за тем, чтобы указатель делений барабана не перескакивал из одной бороздки барабана в другую.
  • 3) Вращая барабан, подвести указатель (в поле зрения окуляра ) к первой красной линии (690,7 нм), затем поочередно к другим линиям. Положение каждой линии определяется по показаниям на шкале барабана и записывается в таблицу 4.1. Следует помнить, что ртутная лампа зажигается только в холодном состоянии, поэтому прежде, чем погасить её, покажите результаты преподавателю.



  • 4) Выключите ртутную лампу с помощью тумблеров "ДРШ” и "СЕТЬ”. Уберите ртутную лампу с оптической скамьи.
  • 5) Установите водородную трубку, включите её нажатием кнопки на столе и не отпускайте в течение времени наблюдения спектра водорода.




  • 6) Выведите в поле зрения последовательно три наиболее интенсивные линии серии Бальмера - красную, сине-зелёную и сине-фиолетовую. Произведите отсчёты α на барабане монохроматора для этих линий. Результаты занесите в таблицу 4.2.

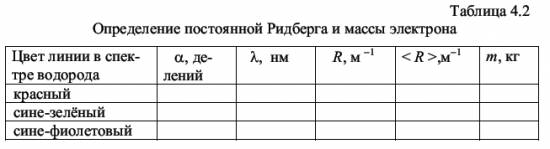
4.4.3. Обработка результатов измерений

  1. По данным измерений α   для спектральных линий ртути постройте на миллиметровой бумаге градуировочный график монохроматора (зависимость α от длины световой волны λ,), откладывая по оси ординат деления барабана а, а по оси абсцисс - соответствующие длины волн λ, (в нм). За начало оси абсцисс при этом удобно взять λ = 400 нм. Критерием правильности построения графика является его плавность и отсутствие изломов и перегибов.
  2. По градуировочной кривой определите длины волн трёх спектральных линий водорода. Результаты запишите в таблицу 4.2.
  3. Вычислите постоянную Ридберга по формуле (4.2) для каждой из трёх спектральных линий водорода.
  4. Вычислите среднее значение постоянной Ридберга <R>
  5. Используя полученное среднее значение постоянной Ридберга, вычислите массу электрона m по формуле (4.14) (h = 6,62 * 10-34 Дж·с, с = 3 · 108 м/с, ε0 =  8,85 · 10-12 Ф/м, е = 1,6 · 10-19 Кл). Результаты вычислений R, <R> и m занесите в таблицу 4.2.

4.5. Контрольные вопросы
  1. Что называется спектром?
  2. Объясните происхождение линейчатых спектров атомов.
  3. Какие закономерности наблюдаются в спектре атомарного водорода?
  4. Как определяется первая линия и граница каждой серии?
  5. Сформулируйте постулаты Бора.
  6. Выведите формулы для радиуса орбиты электрона и энергии электрона на орбите.
  7. В чем состоит принцип соответствия Бора?
  8. Каков физический смысл квантовых чисел?
  9. Объясните различия в схемах энергетических состояний с точки зрения классической теории и квантовой механики.
  10. Какие состояния называются вырожденными?
  11. Какой серии соответствуют переход nd → 2p? С помощью условных обозначений состояний электрона запишите переходы, соответствующие сериям Лаймана, Бальмера, Пашена, ... .
  12. Что значит: проградуировать монохроматор?

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.

  1. Детлаф А.А., Яворский Б.М. Курс физики. М.: Высшая школа, 1989. -стр. 431 - 434; 444 - 452; 455 - 458.
  2. Трофимова Т.И. Курс физики. М.: Высшая школа, 1990. - стр. 334 - 340; 358 - 362.
  3. Савельев И.В. Курс общей физики. В 3-х т. - Т.3. - М.: Наука, 1987. - стр.
Добавил: naddy (09.05.2010) | Категория: Квантовая физика
Просмотров: 11873 | Загрузок: 1 | Рейтинг: 0.0/0 |
Комментарии (0)
Имя *:
Email *:
Код *: