Просвечивание α-частицами металлических пластинок и теория рассеяния α-частиц

16. 2. Содержание работы

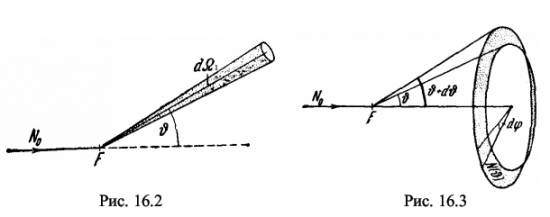
Как показали опыты, проведенные Резерфордом с сотрудниками еще в 1911-13 г. г., параллельный пучок α-частиц, пройдя сквозь слой вещества (тонкий металлический листочек), рассеивается [1,2]. В основном, α-частицы отклоняются на небольшие углы, в среднем 2-3°, и распределение α -частиц по углам в точности следует статистической кривой случайных явлений.

Но наряду с этим некоторое число α -частиц (очень малое - примерно 1 на 8000) рассеивается на большие углы, иногда превышающие 90° и доходящие в некоторых случаях почти до 180°. Детальный анализ результатов показал, что эти большие углы рассеяния для указанного числа α -частиц выходят за рамки накопления случайных малых отклонений и являются результатом единичного соударения (для одной α -частицы).

Резерфорд указал, что это возможно, если внутри атома имеется чрезвычайно сильное электрическое поле, которое создается положительным зарядом, связанным с большой массой и сконцентрированным в очень малом объеме (радиусом порядка 10^-15 м). Отсюда и возникла "ядерная" модель атома, согласно которой атом устроен наподобие планетной системы: малое по размерам, положительно заряженное ядро, в котором сосредоточена почти вся масса атома, и отрицательные электроны, обращающиеся около этого ядра по замкнутым орбитам.

На основании этих представлений Резерфорд развил количественную теорию рассеяния α - частиц. Пусть в точке О (рис. 16.1) помещается рассеивающее ядро.

Обозначим заряд этого ядра через + Ze, где Z - порядковый номер элемента, а е -заряд электрона.

Предположим, что масса указанного ядра настолько больше массы α-частицы, что при взаимодействии с последней ядро можно считать неподвижным. Также предположим, что сила взаимодействия между ядром и α-частицей подчиняется закону Кулона, т.е. что эта сила обратно пропорциональна квадрату расстояния между обеими частицами. Необходимо учитывать, что это последнее предположение на первых порах является только гипотезой и оправдывается лишь последующим согласием теории с экспериментом.

Классическая механика показывает, что при всех этих предположениях α-частица должна описывать относительно ядра О гиперболу. Обозначим массу α-частицы через М, ее заряд + Z_αe, а ее скорость на большом расстоянии от рассеивающего ядра - через v. Если бы α -частица не взаимодействовала с ядром, то она прошла бы на расстоянии p (рис. 16.1) от ядра (так называемое "прицельное рас-стояние").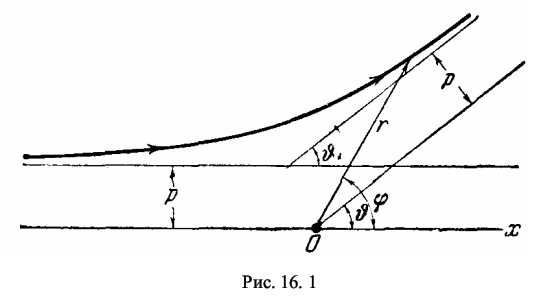



Потенциальная энергия взаимодействия а -частицы в поле неподвижного ядра будет равна

Законы сохранения энергии Е и момента импульса Р дают

где M - масса α-частицы.

После преобразований и введения новой переменной р = 1 / r будем иметь:


Дифференцируя это уравнение еще раз, производя различные сокращения и перестановки, получаем

где
Общее решение уравнения (16.4) таково:



Используем теперь начальные условия. Очевидно (рис. 16.1), что при φ = π r = ∞ и, следовательно, р = 0. Это дает при подстановке в (16.6)


Второе условие мы получим следующим образом. Ордината любой точки траектории связана с r и φ очевидным соотношением y = r · sinφ или

Воспользовавшись (16.6) и (16.7), найдем



Учтем, что при φ = π ордината у равна "прицельному расстоянию" р, а (1 + cosφ) и первый член в правой части обращается в нуль. Мы получаем, таким образом, B = 1 / p, и решение (16.6) принимает окончательный вид

Отклонение а - частицы φ равно углу υ между асимптотами гиперболы, а для направления полета после отклонения р = 0. Поэтому из (16.8) мы получаем



или, принимая во внимание значение С из (16.5),



Наконец, момент импульса Р можно выразить через прицельное расстояние р и скорость v:


Подставив это в (16.10), получим



Это и есть формула для угла отклонения α-частицы в поле ядра, полученная при использовании кулоновских сил отталкивания данных частиц.

Данную формулу невозможно проверить непосредственно экспериментом, так как в нее входит недоступное измерению "прицельное расстояние" p
.
Резерфорд, однако, положил формулу (16.11) в основу статистической теории, которая дает выражение для эффективного сечения рассеяния α -частиц в зависимости от параметров, доступных экспериментальному определению.

Представим себе сферу, в центре которой расположен рассеивающий листок F (рис. 16.2). Пусть на этот листок в единицу времени падает N₀ α -частиц. При детальном изучении рассеяния определяется среднее число частиц N (υ), рассеянных в пределах телесного угла dΩ₁ в направлении, характеризуемом углами υ и φ. Величина телесного угла dΩ₁ равна отношению элемента поверхности сферы к квадрату радиуса






В опытах Резерфорда и его сотрудников чаще изучалось среднее число частиц, рассеиваемых в пределах области, лежащей между двумя телесными углами, характеризуемыми отверстиями υ и υ + dυ (рис. 16.3). Очевидно, что соответствующий этому случаю телесный угол dΩ₂ (или просто dΩ) получится путем интегрирования (16.12) по φ в переделах от 0 до 2π:

Вычислим эффективное сечение для рассеяния в пределах этого телесного угла dΩ. Положим, что α-частицы до рассеяния летят параллельным потоком. Так как при прочих равных условиях угол отклонения α-частицы по формуле (16.11) определяется прицельным расстоянием р, то, очевидно, на угол, лежащий в пределах между υ и υ + dυ, отклонятся α -частицы, у которых прицельное расстояние лежит между р и p - dp, т.е. α -частицы, пролетающие внутри колец между кругами с радиусами, заключенными между р и p - dp , описанными около каждого из рассеивающих центров.

Площадь каждого такого кольца равна 2npdp, и можно утверждать, что среднее число α - частиц, отклоненных на угол между υ и υ + dυ, т.е. летящих после рассеяния внутри телесного угла dΩ, пропорционально 2π · p· dp.

Тогда эффективное сечение ядра da для рассеяния α -частиц равно



Если найти р из (16.11) и возвести его в квадрат, то получим



Дифференцируя, находим следующее выражение:



и, подставляя его в (16.14), получаем




Здесь знак минус не имеет существенного значения: он указывает лишь на то, что с увеличением прицельного расстояния р угол υ уменьшается (и наоборот). Поэтому в дальнейшем используется только абсолютное значение p · d · p . Введем в (16.15) еще телесный угол dΩ по формуле (16.13) и получим:



Это и есть формула Резерфорда для рассеяния α -частиц.

Для сравнения с результатами эксперимента нужно найти макроскопическое сечение ∑, т.е. сумму эффективных сечений всех рассеивающих ядер в 1 м². Если допустить, что все ядра в листке распределены равномерно и не перекрывая друг друга, то очевидно, что



где n - число рассеивающих ядер в 1 м². Пользуясь (16.16), получаем




Если теперь обозначить через N число α-частиц, падающих в 1 секунду на поверхность рассеивающего листка, то среднее число α-частиц, рассеянных на угол υ в пределах телесного угла dΩ, будет, очевидно,




Как видно, число рассеянных α-частиц очень сильно зависит от угла υ и быстро возрастает с уменьшением 0.

Формула Резерфорда была многократно подвергнута тщательной экспериментальной проверке. Из (16.17) следует, что



Таким образом, если, сохраняя все остальные условия, изменять только угол 6, то должно быть



Этот вывод и был проверен в первую очередь еще во времена Резерфорда. Полученные экспериментальные результаты показали: несмотря на то, что даже, если величина 1 / sin⁴ (υ / 2) и число сцинтилляций на люминесцентном экране (от бомбардировки а-частиц) изменяются в очень широких пределах, произведение dN · sin⁴ (υ / 2) остается приблизительно постоянным в согласии с требованием теории.

Аналогичным образом была изучена зависимость рассеяния от толщины листков и от скорости α-частиц. Во всех случаях для рассеяния в листочках из тяжелых металлов установлено хорошее согласие экспериментальных результатов с требованиями теории. Это согласие одновременно является доказательством применимости закона Кулона к взаимодействию между α- частицами и рассеивающими ядрами при тех условиях, в которых были произведены опыты, т.е. для тяжелых ядер и не слишком быстрых α-частиц.

Из этого, однако, не следует делать вывода об универсальной применимости закона Кулона для ядерных взаимодействий. Напротив, изучение рассеяния а-частиц легкими ядрами показало, что когда расстояние между взаимодействующими частицами уменьшается до 10^-14 м, наблюдаются резкие отклонения от закона Кулона, а на расстояниях, меньших 10^-14 м, обнаруживается действие быстро убывающих с расстоянием сил притяжения, перекрывающих действие кулоновских сил отталкивания между одинаково заряженными частицами.

Формула Резерфорда (16.18) позволяет экспериментальным путем найти число Z, т.е. число элементарных положительных зарядов ядра. В самом деле, подсчитывая на флуоресцирующем экране число сцинтилляций N, создаваемых падающими α-частицами, и число сцинтилляций dN, создаваемых α-частицами, рассеянными на угол 3, можно узнать величину dσ = dN / N . В правую же часть формулы Резерфорда (16.18) входят, кроме искомой величины Z, либо величины известные (n, e), либо величины доступные экспериментальному определению (M · υ²).

Таким образом, для отыскания Z нужно произвести подсчет числа сцинтилляций N и dN . Главная трудность эксперимента обусловлена тем, что эти числа очень сильно различаются между собой. В первых опытах числа N и dN измерялись на разных установках, т.е. в разных условиях, что являлось источником значительных ошибок.

Чадвик использовал расположение опыта, при котором оба числа N и dN могут быть измерены на одной и той же установке, вследствие чего ему удалось определить Z с большей точностью. Идея опыта Чадвика заключается в следующем. Рассеивающая фольга имеет вид кольца AА' (рис. 16.4); препарат R и экран S из люминисценого вещества Zn · S устанавливаются на одинаковом расстоянии r от АА' . Измеряется число α -частиц, рассеянных на один определенный угол 0, выбранный (для упрощения расчета) так, чтобы он был вдвое больше угла между осью RS и направлением лучей, идущих от R к фольге (рис. 16.4).

Располагая внутри кольца между R и S экран, непрозрачный для α -частиц, можно было считать одни только рассеянные α -частицы; наоборот, закрывая экраном кольцо АА' можно было считать число частиц N в падающем пучке. Так как это число слишком велико для того, чтобы можно было непосредственно подсчитать сцинтилляции первичных α -частиц на экране, то перед S располагается вращающийся диск с узким вырезом, при помощи которого число сцинтилляций можно было произвольно уменьшать в любое число раз.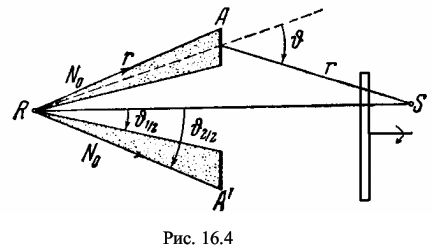



Таким путем Чадвик нашел следующие значения Z для платины, серебра и меди: Pt (78) - 77,4; Ag (47) - 46,3; Сu (29) - 29,3. Числа, стоящие в скобках после химических символов элементов, означают номер места соответствующего эле-мента в периодической системе Менделеева (атомный номер). Таким образом, опыты Чадвика показывают, что число элементарных положительных зарядов яд-ра равно атомному номеру соответствующего элемента.

Результаты опытов Резерфорда и Чадвика, как уже указывалось, легли в основу ядерной модели атома. Эта модель была детализирована и обоснована теоретическими выкладками в 1913 г. Нильсом Бором [3,4].

В основу развитой им квантовой теории строения атома Бор положил следующие два постулата:
1. Электроны в атомах и атомных системах могут пребывать только в определенных стационарных состояниях, в которых они не излучают и не поглощают энергию. В этих состояниях атомные системы обладают энергиями, образующими дискретный ряд: Е1, Е2,...,Еn. Состояния эти характеризуются своей устойчивостью.

Из всех возможных согласно классической механике состояний орбит электронов в атоме осуществляются лишь такие, у которых момент импульса есть величина, кратная h / 2π:



где h = 6,62 · 10^-34 Дж ·• с - постоянная Планка. Величина h / 2π = ђ является квантовой единицей момента импульса, а соотношение (16.^2 называется "правилом квантования".

2. При переходе из одного стационарного состояния в другое атомы испускают или поглощают излучение только строго определенной частоты. Излучение, испускаемое или поглощаемое при переходе из состояния E_m в состояние E_n монохроматично, и его частота v определяется из условия

(условие частот Бора).

Оба эти постулата резко противоречат требованиям классической электродинамики, так как по первому постулату атомы не излучают, несмотря на то, что образующие их электроны совершают ускоренное движение (например, обращение по замкнутым орбитам), а по второму - испускаемые частоты не имеют ничего общего с частотами периодических движений электронов.

Рассмотрим согласно теории Бора [1-4] так называемый «водородоподобный атом», т.е. систему, состоящую из ядра с зарядом +Ze (Z - целое число) и одного электрона. При Z = 1 такая система представляет собой собственно водородный атом, при Z = 2 - однократно ионизированный атом гелия Не⁺, при Z = 3 - двукратно ионизированный атом лития Li⁺⁺ и т.д.

Из опытов Резерфорда по рассеянию а-частиц следует, что закон Кулона имеет место вплоть до расстояния порядка 10^-14 м. Поэтому можно утверждать, что взаимодействие электрона с ядром в модели Бора подчиняется закону Кулона, т.е. сила, с которой ядро удерживает электрон, должна быть равна (kZe²) / r², где k = 1 / (4π · ε₀) = 9 · 10⁹ м / Ф .

Тогда потенциальная энергия электрона:


Кинетическая энергия электрона с массой m (при массе ядра М_Я →∞):


Полная энергия электрона в атоме:

Но при движении электрона по круговой орбите (m · v²) / r= k · (Ze²) / r². Тогда

и, следовательно, полная энергия


Согласно первому постулату Бора (16.19) будем иметь:


Из (16.21) и (16.23) получим дискретные значения радиусов орбит электрона в атоме:

где r₀ = ђ² / (k · m · e²) = 0,529 · 10^-10 м - боковой радиус, n = 1, 2, 3, ... - квантовые числа.

Приравнивая (16.23) и (16.24), получим v_n = (k ·Ze²) / (n ·ђ), т.е. скорость v_n на определенной орбите электрона с квантовым числом п также дискретна.

Используя (16.22) и (16.24), для полной энергии получим дискретные значения:


где Е₁ - энергия электрона в основном состоянии с n = 1.

При переходе атома из состояния Е₂(n₂) в состояние Е₁(n₁) на основании (16.20) и (16.25) излучаемая частота будет равна




где Rv = (k² · m · e⁴) / (4π · ђ³) = (m· e⁴) / (8ε₀² · h³) = 3,29 · 10¹⁵ Гц - постоянная Ридберга.

Также R = Rv / c = 1,097· 10⁷ м^-1 (где с - скорость света в вакууме) и


что точно совпадает с эмпирической формулой Бальмера, описывающей длины волн λ спектральных линий в спектре атома водорода. С учетом движения ядра (с массой М_Я):



где Rv∞ = 3,29 · 10¹⁵ Гц, что также согласуется с экспериментальными значениями.

Эти совпадения говорят о том, что теория Бора достаточно хорошо описывает поведение электрона в водородоподобных атомных системах.

Тем самым, теория Бора явилась весьма крупным шагом в развитии теории строения атома. Она с полной отчетливостью показала неприменимость классической физики к внутриатомным явлениям, с одной стороны, и первенствующее значение квантовых законов в микроскопических системах, - с другой [1]. Наряду с этими и некоторыми другими положительными сторонами теория Бора обладала существенными недостатками.

К числу их относится, прежде всего, внутренняя логическая противоречивость теории. В самом деле, теория Бора не была ни по-следовательно классической, ни последовательно квантовой теорией.

Кроме того, даже в простейшем случае водородоподобных атомов теория Бора позволяла вычислять только частоты спектральных линий, но не их интенсивности. Для вычисления интенсивностей приходилось пользоваться классической электродинамикой.

Особенно серьезной была неудача всех попыток построения на основании теории Бора нейтрального атома гелия - одного из простейших атомов периодической системы, непосредственно следующего за атомом водорода и состоящего из трех частиц - ядра и двух электронов.

Поэтому после открытия своеобразных волновых свойств вещества стало совершенно ясно, что теория Бора, опирающаяся на классическую механику, могла быть только переходным этапом к созданию последовательной квантовой теории атомных явлений.