Поведения микрочастиц вблизи потенциального барьера

15.1. Цель работы

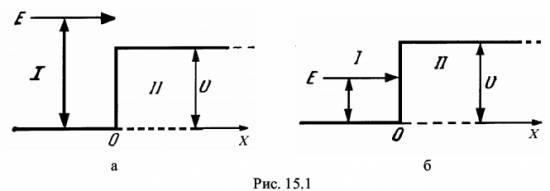
Методом расчета на персональном компьютере изучить особенности по-ведения микрочастиц вещества вблизи одномерных потенциальных барьеров раз-личных размеров и оценить характеристики «туннельного эффекта» при про-хождении этих барьеров.

15.2. Содержание работы

Движение и поведение микрочастиц вещества в квантовой механике хорошо описывается с помощью уравнения Шрёдингера и его решения. Одним из распространенных случаев такого подхода является решение задачи о поведении частицы на границе раздела двух или нескольких областей, в каждой из которых потенциальная энергия частицы постоянна, но различается на конечную величину [1].

Схематизируя реально встречающиеся условия, предположим, что на границе областей I и II потенциальная энергия изменяется скачком, как показано на рисунке 15.1, а, б.



Выберем ось Х в направлении движения частицы массой т и тогда будем описывать её поведение волновой функцией Ψ = Ψ(x). Уравнение Шрёдингераможно записать для такого случая в виде



где ђ = h / 2π - постоянная Планка;
Е - энергия частицы;
U - потенциальная энергия зоны, причем в зоне I при х < 0 имеем U = 0, а в зоне II при х > 0 имеем U = U₀ = const.

Детальное решение уравнения Шрёдингера (15.1) для зон I и II дает следующие общие уравнения для волновых функций в каждой из зон [1,2]:


Здесь k₁ = (1 / ђ) · (2m · E)^1/2, a k₂ = (1 / ђ) · (2m · (E - U))^1/2 - волновые числа волн де-Бройля в соответствующих зонах I и II.

Рассмотрим условия перехода частиц из области I в область II в обоих случаях, представленных на рис. 15.1, а и 15.1, б.

При Е > U (см. рис. 15.1, а) частица, подчиняющаяся классической механике, обязательно перейдет из области I в область II, преодолев задерживающее поле с энергией U, и будет двигаться в области II с уменьшенной энергией (Е - U).

Частица, подчиняющаяся квантовой механике, будет в этом случае вести себя совершенно иначе. Это связано, прежде всего, с характером решения уравнения Шрёдингера (15.2), в котором первый член описывает падающую волну де-Бройля, распространяющуюся в направлении оси X, а второй член - отраженную волну де-Бройля. При этом следует заметить, что в зоне I могут распространяться как падающая, так и отраженная волны, а в зоне II - лишь проходящая волна (так как для отражения в этой зоне нет причин - нет границы раздела). Поэтому в (15.3) следует положить в₂ = 0 и тогда

Если положить амплитуду падающей волны а₁ = 1, то можно вычислить остальные амплитуды в₁ и а₂, применяя граничные условия. Расчет дает [1], что



Следовательно, для коэффициентов отражения R и прозрачности D , которые по аналогии с оптикой пропорциональны квадратам соответствующих амплитуд (с учетом, что a₁² = 1), будем иметь

и

Эти коэффициенты можно истолковать с корпускулярной точки зрения следующим образом: R представляет вероятность частице испытать отражение на границе раздела областей, a D - вероятность пройти в область П или, как принято говорить, преодолеть потенциальный барьер. Как и следовало
ожидать при этом R + D = 1, что вытекает из подстановки в это выражение формул (15.5) и (15.6).

Расчет коэффициентов R и D по этим же формулам показывает, что, когда энергия частицы вдвое больше высоты потенциальной ступени U, вероятность отражения имеет заметную величину (около 3%). Эта вероятность вырастает еще больше при уменьшении соотношения E / U.

При Е < U (см. рис.15.1, б) переход из области I в П по классической механике невозможен, т.к. при этом условии потенциальная энергия частицы больше полной, а значит кинетическая энергия должна была бы стать отрицательной и скорость - мнимой.

Расчет по квантовой механике коэффициента отражения R для этого случая дает

где


Следовательно, отражение в этом случае является полным (R = 1, D = 0), что вполне соответствует ожидаемому результату. Однако при этом (как показывает детальный расчет Ψ - функции) имеется определенная вероятность найти частицу в области II:


Правда, эта вероятность экспоненциально (т.е. очень быстро) убывает с увеличением х, но она отлична от нуля. Значит, микроскопические частицы могут проникать в области "запрещенные" для частиц макроскопических. Оценочный расчет дает, например, что относительная вероятность найти электрон на расстоянии 10^-10м от границы при условии, если (U - Е) = 1 эВ, составляет 29%, т.е. очень большая. Однако уже при х = 5 ·10^-10 м эта вероятность становится равной лишь 0,5%.

Теперь рассмотрим поведение микрочастиц вблизи потенциального барьера конечной ширины d (см. рис.15.2). Предположим, что частица движется слева направо параллельно оси Х в поле, которое мы разделим на три области.

В области I, т.е. при х < 0, потенциальная энергия U = 0;
в области II, т.е. при 0 < x < d,- U = const ≠ 0;
в области III, т.е. при х > d,- U = 0.

Этот тип барьера схематически представляет условия, встречающиеся при решении многих задач атомной физики.

Напишем уравнение Шрёдингера для каждой области отдельно: для областей I и III (U = 0):


и для области II (U ≠ 0):



Решения этих уравнений будут соответственно: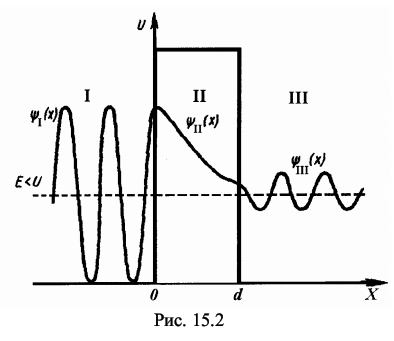





Отличие рассматриваемого случая от изученного ранее (на основании рис. 15.1) состоит в том, что теперь (см. рис. 15.2) отражение имеет место как на границе областей I и II, так и на границе областей II и III. В соответствии с этим решениями будут:



При этом, как и ранее, коэффициент а₁ положен равным единице. Графики Ψ - функций для каждой из зон I, II, III, соответственно, представлены на рис. 15.2 в виде сплошных линий.

Для вычисления коэффициентов R и D необходимо найти прежде всего постоянные b₁, b₂, a₂, а₃. С этой целью можно воспользоваться условиями непрерывности функции Ψ и ее первой производной на границах областей I и II, II и III, т.е. при х = 0 и при х = d. Выпишем эти условия:




Эти условия дают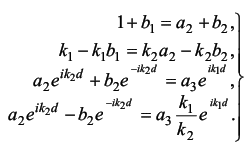


Решая эту систему уравнений, найдем следующее выражение для а₃: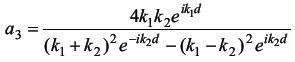



Коэффициент прозрачности барьера D [см. формулу (15.6)] в данном случае равен просто квадрату модуля а₃ ввиду того, что длина волны в областях I и III - одна и та же:


Представляет интерес величина D в том случае, когда Е < U. При этом


будет, очевидно, чисто мнимым числом. Положим


где

Экспоненциальные функции  e^{±i · k₂ · d} , входящие в знаменатель выражения (15.17), будут при этом условии действительными числами e^{± k · d}. Вместо формулы (15.17) мы получим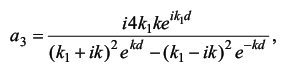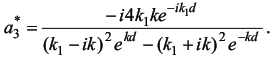



Дальнейший расчет дает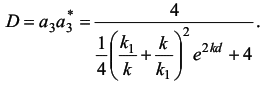



Можно заметить, что слагаемым 4 в знаменателе формулы (15.20) можно пренебречь по сравнению с e^2kd и, так как k₁ и k одного порядка величины, то с точностью до несущественного множителя:




Эта формула показывает, что проницаемость барьера в очень сильной степени зависит от его ширины d Оценка величины D для разных значений ширины барьера показывает, что проницаемость довольно велика (несколько процентов) для барьеров атомных размеров (~10^-10 м), но уже для d = 10^-9 м она становится ничтожно малой.

Интересно отметить, что прохождение через потенциальный барьер не сопровождается для частицы потерей энергии: она выходит из пределов барьера с той же энергией, с какой в него попадает.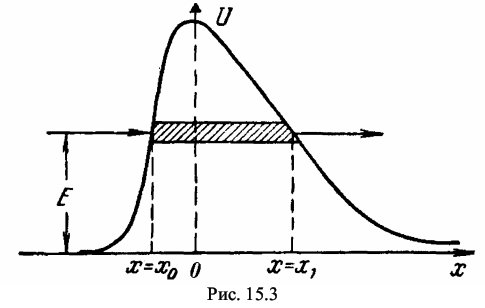



Мы рассмотрели случай прохождения частицы через потенциальный барьер весьма упрощенной прямоугольной формы. Можно показать, что коэффициент прозрачности барьера произвольного вида (см. рис 15.3) выражается с достаточным приближением формулой, которая является естественным обобщением формулы (15.21),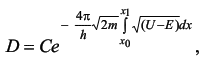


где С - несущественная постоянная порядка единицы.

Прохождение через потенциальный барьер часто образно называют «туннельным эффектом»: для преодоления барьера частица не взбирается на его вершину, но проходит под ней как бы через туннель.

Многие явления, недоступные для объяснения в классической механике, лег-ко объясняются в квантовой механике именно благодаря «туннельному эффекту» (например, эмиссия электронов из металлов, явления в контактном слое на границе двух полупроводников, α - распад, протекание термоядерных реакций).