Изучение закономерностей внешнего фотоэффекта
|
2.1. Цель работы
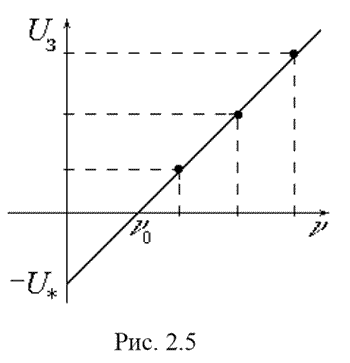
Практическое ознакомление с закономерностями внешнего фотоэффекта; экспериментальное определение работы выхода для сурьмяно-цезиевого фотокатода, а также постоянной Планка. 2.2. Содержание работы 2.2.1. Явление внешнего фотоэффекта Внешним фотоэлектрическим эффектом (фотоэффектом) называется испускание электронов веществом под действием света. Фотоэффект используется в фотоэлементах, получивших широкое распространение как регистрирующие приборы в самых разных областях науки и техники. Изучение закономерностей фотоэффекта привело физическую науку к понятию световых квантов и сыграло выдающуюся роль в становлении современных представлений о природе. 2.2.2. Вакуумный фотоэлемент Это один из самых распространенных приборов, использующих внешний фотоэффект. Он представляет собой откаченный стеклянный баллон, часть внутренней поверхности которого покрыта металлом и является катодом К. Металлическое кольцо А служит анодом (см. рис. 2. 1). 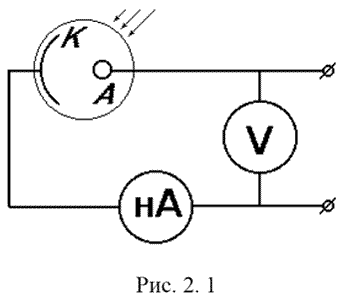 Электрическая цепь на рис. 2. 1 разомкнута; ток в ней появится, только если из катода будут вырваны (например, светом) электроны, которые затем достигнут анода. Сила фототока зависит от числа вылетающих из катода электронов, от их начальной скорости, а также от разности потенциалов между катодом и анодом. Зависимость силы фототока от анодного напряжения (при постоянной освещенности катода) называется вольтамперной характеристикой (ВАХ) фотоэлемента (см. рис. 2. 2). 2.2.3. Закономерности фотоэффекта Даже при нулевом анодном напряжении U некоторые из фотоэлектронов долетают до анода, поэтому I ≠ 0 при U = 0. С увеличением U анода достигают все большее число электронов, и сила фототока постепенно возрастает. Наконец, при некотором напряжении (называемым напряжением насыщения UН) все фотоэлектроны долетают до анода, и в дальнейшем увеличение напряжения не приводит к увеличению силы тока. Достигнутое значение силы фототока называется током насыщения IН. По значению силы тока насыщения можно судить о количестве электронов n , испускаемых катодом за единицу времени: IН = n*е (2. 1) Если анодное напряжение отрицательно, то оно будет тормозить фотоэлектроны, и сила тока уменьшится. При некотором значении напряжения U = UЗ < 0 (которое называется запирающим) даже самые быстрые фотоэлектроны не в силах достигнуть анода, и ток прекращается. При этом вся начальная кинетическая энергия электронов расходуется на совершение работы против сил задерживающего электрического поля: Ekmax = e*UЗ (Ekmax – начальная кинетическая энергия самых быстрых фотоэлектронов, покидающих катод при данных условиях). (2.2) На рис. 2. 2 приведены несколько ВАХ одного и того же фотоэлемента, полученные при облучении катода монохроматическим светом одной и той же частоты ω, но разной интенсивности (а) или одной и той же интенсивности I, но разных частот (б). 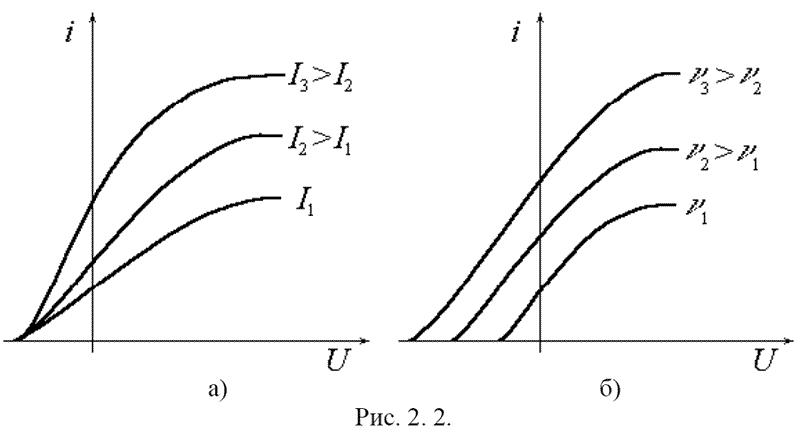 Экспериментально установлены следующие закономерности фотоэффекта [1]. 1. При фиксированной частоте света сила фототока насыщения (и число фотоэлектронов вырываемых из катода за единицу времени) прямо пропорционально интенсивности света). 2. Величина запирающего напряжения (и максимальная скорость фотоэлектронов) определяется частотой света и не зависит от его интенсивности. 3. Для каждого вещества существует красная граница фотоэффекта, т.е. минимальная частота света ω0, при которой фотоэффект еще возможен. 2.2.4. Недостаточность классических представлений К моменту открытия фотоэффекта была общепризнана волновая теория света, берущая начало из опытов Френеля, Юнга и Араго по дифракции и интерференции света. Из уравнений Максвелла следовало существование электромагнитных волн, свойства которых (экспериментально изученных Герцем) оказались тождественны свойствам света, а также инфракрасного и ультрафиолетового излучений. Были измерены длины световых волн (0,4 – 0,7 мкм). С помощью представлений о свете как об электромагнитных волнах успешно объяснены (не только качественно, но и количественно) закономерности отражения, преломления, поляризации света. Естественным было стремление объяснить с тех же позиций и фотоэффект. Металлы отличаются от других веществ наличием большого числа "свободных" электронов (не связанных с каким-либо атомом) проводимости. Резонно предположить, что именно эти электроны и будут вырываться электрическим полем световой (электромагнитной) волны. Тогда первый из указанных в п.2.2.3 законов фотоэффекта объясняется элементарно: чем больше амплитуда световой волны, тем большее количество электронов может она вырвать с поверхности металла. Найдем далее зависимость скорости и кинетической энергии приобретаемой электроном, от параметров световой волны. Для этого проинтегрируем уравнение движения "свободного" электрона проводимости в переменном электрическом поле волны: me*v' = cos(ω*t) (2.3) где Е – амплитуда, ω = 2πν − циклическая частота света. Получим me*v = (e*E) / ω * sin(ω*t) Ek = me*v2/2 = 1/2*me * ( e*E / ω )2 * sin2(ω*t)(2.4) (2.5) Поскольку интенсивность света определяется квадратом амплитуды электрического вектора Е, то можно сказать, что максимальная начальная кинетическая энергия фотоэлектронов: во-первых, прямо пропорциональна интенсивности света; во-вторых, обратно пропорциональна квадрату частоты света. Однако оба этих предсказания никак не подтверждаются наблюдениями! Даже если предположить, что свет вырывает из металла не электроны проводимости, а электроны, связанные с атомами квазиупругими силами, то решение уравнения движения такого электрона дало бы резонансную зависимость Еkmax от ω (острый пик при ω = ω0 – частота собственных колебаний электронов в атомах) и по-прежнему пропорциональность меду интенсивностью света и Еkmax. Итак, классические представления явно не способы объяснить всех наблюдаемых закономерностей фотоэффекта! 2.2.5. Квантовое истолкование законов фотоэффекта В 1905 г. Эйнштейн показал, что закономерности излучения и поглощения света легко могут быть объяснены в предположении, что энергия света излучается и поглощается дискретными порциями (квантами); при этом величина кванта энергии света прямо пропорциональна его частоте: ε = hν (коэффициент h называется постоянной Планка). В соответствии с квантовой теорией (см., например [2], [3]) энергия электрона в твердом теле также принимает дискретный ряд значений. Эти значения (энергетические уровни) группируются в полосы, или разрешенные зоны разделенные запрещенными зонами. Энергетическая зона, заполненная электронами лишь частично, называется зоной проводимости; у зон, лежащих ниже неё, заполнены все уровни. Находящиеся в зоне проводимости электроны легко могут переходить на более высокие энергетические уровни этой зоны, иначе говоря – увеличивать свою кинетическую энергию (ускоряться) за счет внешних воздействий. Наивысший из энергетических уровней, занятых электронами при Т = 0 К, называется уровнем Ферми. При обычных условиях все электроны в металле имеют отрицательные значения полной энергии; за нулевой уровень энергии принимается энергия покоящегося электрона, находящегося вне металла. Наименьшая работа, необходимая для удаления электрона из металла в вакуум, называется работой выхода А0. Фактически работа выхода – это энергия, которую нужно затратить, чтобы вырвать из металла (при Т = 0 К) электрон, имеющий энергию Ферми и движущийся к поверхности (а не вглубь) металла. Для вырывания любого другого электрона понадобится большая энергия! Работу выхода можно также трактовать как глубину потенциальной ямы, в которой находится электроны металла. Она определяется химической природой вещества и в меньшей степени – условиями, в которых оно находится, например, температурой. Если энергия каждого кванта света (фотона) меньше работы выхода, то электроны, которым передается их энергия, не смогут покинуть металл. Минимальная частота света, которая еще может вызывать фотоэффект, определяется соотношением: ν0 = A0 / h (2.6) и называется красной границей фотоэффекта. (Здесь "красная" является синонимом слов "длинноволновая" или "низкочастотная"; красная граница может лежать и в ультрафиолетовой области спектра!) Итак, если поверхность металла освещена светом с частотой ν > ν0, то максимальная кинетическая энергия, которую могут иметь фотоэлектроны, определяется из соотношения Еkmax = h*ν − A0 называемого уравнением Эйнштейна для фотоэффекта. (2.7) В соответствии с уравнением Эйнштейна и формулой (2.2) запирающее напряжение должно зависеть от частоты линейно: е*UЗ = hν − A0 (2.8) Этот вывод (одно из предсказаний квантовой теории) находится в прекрасном соответствии с опытом. Более того, измерив значение запирающего напряжения для нескольких частот света, мы можем с помощью уравнения (2.8) найти работу выхода материала фотокатода и постоянную Планка. 2.3. Описание лабораторной установки В лабораторной установке, показанной на рис. 2.3, в качестве источника света используется ртутная газоразрядная лампа ДРШ, излучающая линейчатый спектр. (Длины волн спектральных линий ртути хорошо известны и занесены в таблицы, что избавляет от необходимости их измерять.) 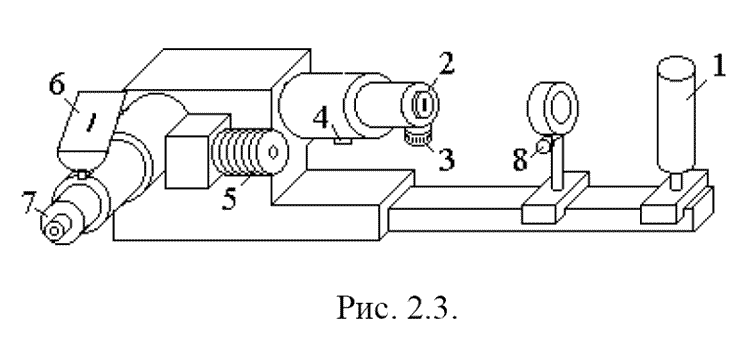 С помощью монохроматора из излучения ртутной лампы выделяется узкие пучки монохроматического света, которые поочередно направляют на фотоэлемент с сурьмяно-цезиевым катодом. 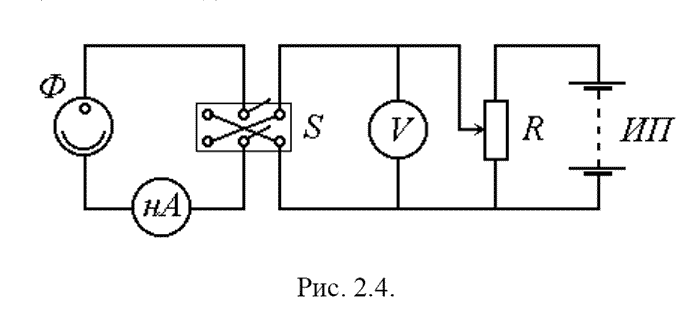 Электрическая схема включения фотоэлемента показана на рис. 2.4. С помощью источника постоянного тока ИП, смонтированного в основании монохроматора, и двухполюсного переключателя S на аноде фотоэлемента Ф можно создавать как положительный (ускоряющее поле), так и отрицательный потенциал (тормозящее поле). Напряжение между катодом и анодом регулируется потенциометром R; для измерения напряжения служит вольтметр V. Сила тока в цепи фотоэлемента измеряется амперметром А. 2.4. Методика проведения эксперимента и обработка результатов 2.4.1. Методика эксперимента 2.4.1.1. Измеряемые и вычисляемые величины Для определения красной границы фотоэффекта и постоянной Планка измеряются значения запирающего напряжения для нескольких наиболее ярких спектральных линий, двигаясь от фиолетовой до желто-зеленой области спектра. Для этих же линий снимаются вольт-амперные характеристики в интервале напряжения от 0 до 3 В. По окончании измерений строится график зависимости UЗ(ν); по графику определяются значения h и ν0. Вычисляются значения λ0 (нм), а также А0 (Дж, эВ). 2.4.1.2. Темновой ток фотоэлемента и точность измерений В реальном фотоэлементе даже при нулевой освещенности катода течет некоторый (очень небольшой) темновой ток IТ, обусловленный отчасти термоэлектронной эмиссией с катода, отчасти разностью работ выхода для катода и анода, отчасти просто утечкой тока между выводами фотоэлемента. При разности потенциалов между катодом и анодом, близкой к UЗ, сила тока в цепи анода того же порядка, что и темновой ток. Однако величина темнового тока зависит от множества параметров и в принципе может меняться в ходе опыта. Из сказанного ясно, что способ экспериментального определения UЗ как напряжения, при котором ток на выходе фотоэлемента равен нулю (или даже предварительно измеренному значению IТ) не вполне надежен. Для получения более достоверного значения UЗ следует увеличивать (по модулю) отрицательное анодное напряжение до тех пор, пока не прекратит уменьшаться анодный ток фотоэлемента. При положительных значениях анодного напряжения темновой ток составляет незначительную часть полного тока. Поэтому при снятии вольт-амперной характеристики в области U > 0 учет темнового тока не требуется. 2.4.2. Порядок выполнения работы 2.4.2.1. Подготовка к работе
2.4.2.2. Измерение запирающего напряжения
2.4.2.3. Снятие вольт-амперных характеристик
Внимание! Измерения по пункте 3 необходимо проделать также для синей (λ = 435,6 нм) и голубой (481,6 нм) линий спектра ртути. Однократно измеряемые величины: Таблица 2.1
2.4.3. Обработка результатов измерений
Измерение задерживающего напряжения Таблица 2.2
 Снятие вольт-амперных характеристик Таблица 2.3
2.5 Контрольные вопросы
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Автор методики: Подопригора А.Г.; ВолгГТУ Добавил: COBA (27.02.2010) | Категория: Квантовая физика Просмотров: 24347 | Загрузок: 1 | Рейтинг: 5.0/4 | Теги: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Комментарии (3) | |||
| |||

 Очень полезная статья. А то обычно если что-то надо по физике, то этого не доищешься. Жалко, что у нас этот предмет закончился.
Очень полезная статья. А то обычно если что-то надо по физике, то этого не доищешься. Жалко, что у нас этот предмет закончился.