Уравнение Шредингера

8.2. Содержание работы

Движение микрочастиц в различных силовых полях описывается в рамках нерелятивистской квантовой механики с помощью уравнения Шредингера, из которого вытекают наблюдаемые на опыте волновые свойства частиц. Это уравнение, как и все основные уравнения физики, не выводятся, а постулируется. Его правильность подтверждается согласием результатов расчета с опытом. Волновое уравнение Шредингера имеет следующий общий вид [1,2]:




где ħ = h / 2π, h = 6,623∙10^-34 Дж ∙ с - постоянная Планка;
m - масса частицы;
∆ - оператор Лапласа (∆ = ∂² / ∂x² + ∂² / ∂y² + ∂² / ∂z²);
ψ = ψ ( x, y, z, t ) - искомая волновая функция;
U ( x, y, z, t ) - потенциальная функция частицы в силовом поле, где она движется;
i - мнимая единица.

Это уравнение имеет решение лишь при условиях, накладываемых на волновую функцию:

1. ψ ( x, y, z, t ) должна быть конечной, однозначной и непрерывной;
2. первые производные от нее должны быть непрерывны;
3. функция | ψ |² должна быть интегрируема, что в простейших случаях сводится к условию нормировки вероятностей.

Для многих физических явлений, происходящих в микромире, уравнение (8.1) можно упростить, исключив зависимость ψ от времени, т.е. найти уравнение Шредингера для стационарных состояний с фиксированными значениями энергии. Это возможно, если силовое поле, в котором частица движется, стационарно, т.е. U = U ( x, y, z ) не зависит явно от времени и имеет смысл потенциальной энергии. Тогда после преобразований можно прийти к уравнению Шредингера для стационарных состояний:




где ψ = ψ ( x, y, z ) - волновая функция только координат;
E - параметр уравнения - полная энергия частицы.

Для этого уравнения реальный физический смысл имеют лишь такие решения, которые выражаются регулярными функциями ψ (называемыми собственными функциями), имеющими место только при определенных значениях параметра E, называемого собственным значением энергии. Эти значения E могут образовывать как непрерывный, так и дискретный ряд, т.е. как сплошной, так и дискретный спектр энергий.

Для какой-либо микрочастицы при наличии уравнения Шредингера типа (8.2) задача квантовой механики сводится к решению этого уравнения, т.е. нахождению значений волновых функций ψ = ψ ( x, y, z ), соответствующих спектру собственных энергией E. Далее находится плотность вероятности | ψ |², определяющая в квантовой механике [1] вероятность нахождения частицы в единичном объеме в окрестности точки с координатами ( x, y, z ).

Одним из простейших случаев решения уравнения Шредингера является задача о поведении частицы в одномерной прямоугольной "потенциальной яме" с бесконечно высокими "стенками". Такая "яма" для частицы, движущейся только вдоль оси Х, описывается потенциальной энергией вида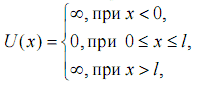




где l - ширина "ямы", а энергия отсчитывается от ее дна (рис. 8.1).

Уравнение Шредингера для стационарных состояний в случае одномерной задачи запишется в виде: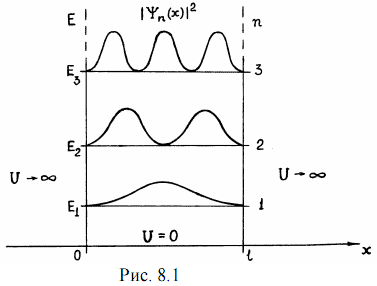





В силу того, что "стенки ямы" бесконечно высокие, частица не проникает за пределы "ямы". Это приводит к граничным условиям:


В пределах "ямы" (0 ≤ x ≤ l ) уравнение (8.4) сводится к виду:



или




Решение уравнения (8.7) с учетом граничных условий (8.5) имеет в простейшем случае вид:




при целочисленных значениях n.

Из выражений (8.8) и (8.10) следует, что


т.е. энергия стационарных состояний зависит от целого числа n (называемого квантовым числом) и имеет определенные дискретные значения, называемые уровнями энергии.

Следовательно, микрочастица в "потенциальной яме" с бесконечно высокими "стенками" может находится только на определенном энергетическом уровне E_n, т.е. в дискретных квантовых состояниях n.

Подставив выражение (8.10) в (8.9) найдем собственные функции


Постоянная интегрирования А найдется из квантовомеханического (вероятностного) условия нормировки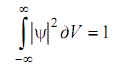




которое для данного случая запишется в виде: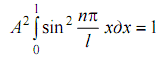




Откуда в результате интегрирования получим А = √ (2 / l ) и тогда имеем




Графики функции ψ_n ( х ) не имеют физического смысла, тогда как графики функции | ψ_n |² показывают распределение плотности вероятности обнаружения частицы на различных расстояниях от "стенок ямы"(рис. 8.1). Как раз эти графики (как и ψ_n ( х ) - для сравнения) изучаются в данной работе и наглядно показывают, что представления о траекториях частицы в квантовой механике несостоятельны.

Из выражения (8.11) вытекает, что энергетический интервал между двумя соседними уровнями равен

Отсюда видно, что для микрочастиц (типа электрона) при больших размерах "ямы" ( l≈ 10^-1м ), энергетические уровни располагаются настолько тесно, что образуют практически непрерывный спектр. Такое состояние имеет место, например, для свободных электронов в металле. Если же размеры "ямы" соизмеримы с атомными ( l ≈ 10^-10 м ), то получается дискретный спектр энергии (линейчатый спектр). Эти виды спектров также могут быть изучены в данной работе для различных микрочастиц.

Другим случаем поведения микрочастиц (как, впрочем, и микросистем - маятников), часто встречаемым на практике (и рассматриваемым в этой работе), является задача о линейном гармоническом осцилляторе в квантовой механике.

Как известно, потенциальная энергия одномерного гармонического осциллятора массой m равна [1, 2]




где ω₀ - собственная частота колебаний осциллятора ω₀ = √ ( k / m);
k - коэффициент упругости осциллятора.

Зависимость (8.17) имеет вид параболы, т.е. "потенциальная яма" в данном случае является параболической (рис. 8.2).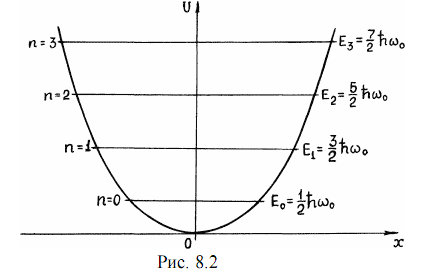


Квантовый гармонический осциллятор описывается уравнением Шредингера (8.2), учитывающим выражение (8.17) для потенциальной энергии. Решение этого уравнения записывается в виде [3]:




где N_n - постоянный нормирующий множитель, зависящий от целого числа n;
α = ( m ∙ ω₀ ) / ħ;
H_n ( x ) - полином степени n, коэффициенты которого вычисляются при помощи рекуррентной формулы при различных целочисленных n.
В теории дифференциальных уравнений можно доказать, что уравнение Шредингера имеет решение (8.18) лишь для собственных значений энергии:


где n = 0, 1, 2, 3... - квантовое число.

Это значит, что энергия квантового осциллятора может принимать лишь дискретные значения, т.е. квантуется. При n = 0 имеет место E₀ = ( ħ ∙ ω_{0 )} / 2, т.е. энергия нулевых колебаний, что является типичным для квантовых систем и представляет собой прямое следствие соотношения неопределенности.

Как показывает детальное решение уравнения Шредингера для квантового осциллятора [3], каждому собственному значению энергии при разных n соответствует своя волновая функция, т.к. от n зависит постоянный нормирующий множитель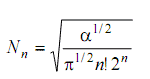



а также H_n ( x ) - полином Чебышева-Эрмита степени n.
При том первые два полинома равны:



Любой последующий полином связан с нми по следующей рекуррентной формуле:



Собственные функции типа (8.18) позволяют найти для квантового осциллятора плотность вероятности нахождения микрочастицы как | ψ_n (х) |² и исследовать ее поведение на различных уровнях энергии. Решение этой задачи затруднительно ввиду необходимости использования рекуррентной формулы. Эта задача успешно может решаться лишь с использованием ЭВМ, что и делается в настоящей работе.