Электропроводность металлов и полупроводников

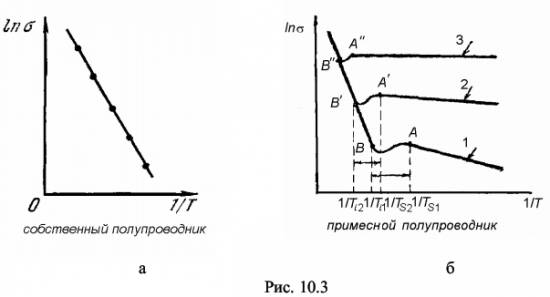
Содержание работы

Электропроводность есть способность тела пропускать электрический ток под действием электрического поля. Для характеристики этого явления служит величина удельной электропроводности σ. Как показывает теория [1-3], величину σ можно выразить через концентрацию n свободных носителей заряда, их заряд е, массу m, время свободного пробега τ_e, длину свободного пробега λe и среднюю дрейфовую скорость < v > носителей заряда. Для металлов в роли свободных носителей заряда выступают свободные электроны, так что:




где u - подвижность носителей, т.е. физическая величина, численно равная дрейфовой скорости, приобретенной носителями в поле единичной напряженности , а именно



В зависимости от σ все вещества подразделяются; на проводники - с σ > 10⁶ (Ом · м)^-1, диэлектрики - с σ > 10^-8 (Ом · м)^-1 и полупроводники - с промежуточным значением σ.

С точки зрения зонной теории деление веществ на проводники, полупроводники и диэлектрики определяется тем, как заполнена электронами при 0 К валентная зона кристалла: частично или полностью.

Энергия, которая сообщается электронам даже слабым электрическим полем, сравнима с расстоянием между уровнями в энергетической зоне. Если в зоне есть свободные уровни, то электроны, возбужденные внешним электрическим полем, будут заполнять их. Квантовое состояние системы электронов будет изменяться, и в кристалле появится преимущественное (направленное) движение электронов против поля, т.е. электрический ток. Такие тела (рис.10.1,а) являются проводниками.

Если валентная зона заполнена целиком, то изменение состояния системы электронов может произойти только при переходе их через запрещенную зону. Энергия внешнего электрического поля такой переход осуществить не может. Перестановка электронов внутри полностью заполненной зоны не вызывает изменения квантового состояния системы, т.к. сами по себе электроны неразличимы.

В таких кристаллах (рис. 10.1,б) внешнее электрическое поле не вызовет появление электрического тока, и они будут непроводниками (диэлектриками). Из этой группы веществ выделены те у которых ширина запрещенной зоны ΔE ≤ 1 эВ (1эВ = 1,6 · 10^-19 Дж).

Переход электронов через запрещенную зону у таких тел можно осуществить, например, посредством теплового возбуждения. При этом освобождается часть уровней - валентной зоны и частично заполняются уровни следующей за ней свободной зоны (зоны проводимости). Эти вещества являются полупроводниками.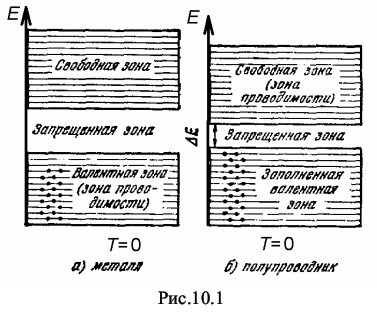

Согласно выражению (10.1) изменение электропроводности (электрического сопротивления) тел с температурой может быть вызвано изменением концентрации n носителей заряда или изменением их подвижности u .

Металлы

Квантово-механические расчеты показывают, что для металлов концентрация n свободных носителей заряда (электронов) равна:


где ђ = h / 2π = 1,05 · 10^-34 Дж · с - нормированная постоянная Планка, E_F - энергия Ферми.

Так как E_F практически от температуры T не зависит, то и концентрация носителей заряда от температуры не зависит. Следовательно, температурная зависимость электропроводности металлов будет полностью определяться подвижностью u электронов, как и следует из формулы (10.1). Тогда в области высоких температур




а в области низких температур

Степень подвижности носителей заряда будет определяться процессами рассеяния, т.е. взаимодействием электронов с периодическим полем решетки. Так как поле идеальной решетки строго периодическое, а состояние электронов - стационарное, то рассеяние (возникновение электрического сопротивления металла) может быть вызвано только дефектами (примесными атомами, искажениями структуры и т.д.) и тепловыми колебаниями решетки (фононами).

Вблизи 0 К , где интенсивность тепловых колебаний решетки и концентрация фононов близка к нулю, преобладает рассеяние на примесях (электрон-примесное рассеяние). Проводимость при этом практически не меняется, как следует из формулы (10.4), а удельное сопротивление

имеет постоянное значение, которое называется удельным остаточным сопротивлением ρ_ост или удельным примесным сопротивлением ρ_прим, т.е.



В области высоких температур у металлов становится преобладающим электрон-фононный механизм рассеяния. При таком механизме рассеяния электропроводность обратно пропорциональна температуре, как видно из формулы (10.3), а удельное сопротивление прямо пропорционально температуре:

График зависимости удельного сопротивления ρ от температуры приведен на рис. 10.2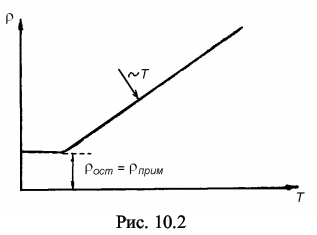


ρ = ρ_прим + ρ_ф


Выражение (10.6) представляет собой правило Матиссена об аддитивности сопротивления. Следует отметить, что как электрон-фононное, так и электрон-примесное рассеяние носит хаотический характер.

Полупроводники

Квантово-механические расчеты подвижности носителей в полупроводниках показали, что, во-первых, с повышением температуры подвижность носителей u убывает, и решающим в определении подвижности является тот механизм рассеяния, который обуславливает наиболее низкую подвижность. Во-вторых, зависимость подвижности носителей заряда от уровня легирования (концентрации примесей) показывает, что при малом уровне легирования подвижность будет определяться рассеянием на колебаниях решетки и, следовательно, не должна зависеть от концентрации примесей.

При высоких уровнях легирования она должна определяться рассеиванием на ионизированной легирующей примеси и уменьшаться с увеличением концентрации примеси. Таким образом, изменение подвижности носителей заряда не должно вносить заметного вклада в изменение электрического сопротивления полупроводника.

В соответствии с выражением (10.1) основной вклад в изменение электропроводности полупроводников должно вносить изменение концентрации п носителей заряда [1-3].

Главным признаком полупроводников является активационная природа проводимости, т.е. резко выраженная зависимость концентрации носителей от внешних воздействий, как-то температуры, облучения и т.д. Это объясняется узостью запрещенной зоны (ΔЕ < 1 эВ) у собственных полупроводников и наличием дополнительных уровней в запрещенной зоне у примесных полупроводников.

Электропроводность химически чистых полупроводников называется собственной проводимостью. Собственная проводимость полупроводников возникает в результате перехода электронов (n) с верхних уровней валентной зоны в зону проводимости и образованием дырок (p) в валентной зоне:

где n_n и· n_ρ - концентрация электронов и дырок,
u_n и u_ρ - соответственно их подвижности,
e - заряд носителя.

С повышением температуры концентрация электронов в зоне проводимости и дырок в валентной зоне экспоненциально возрастает:




где n_nо и n_pо - концентрации электронов и дырок при Т → ∞,
k = 1,38 · 10^–23 Дж/ К - постоянная Больцмана.

На рисунке 10.3,а приведен график зависимости логарифма электропровод-ности ln σ собственного полупроводника от обратной температуры 1 / Т : ln σ = = ƒ(1 / Т). График представляет собой прямую, по наклону которой можно опреде-лить ширину запрещенной зоны ∆Е.


Электропроводность легированных полупроводников обусловлена наличием в них примесных центров. Температурная зависимость таких полупроводников определяется не только концентрацией основных носителей, но и концентрацией носителей, поставляемых примесными центрами. На рис. 10.3,б приведены графики зависимости ln σ = ƒ (1 / Т) для полупроводников с различной степенью легирования (n1 < n2 < n3, где n – концентрация примеси).

Для слаболегированных полупроводников в области низких температур преобладают переходы с участием примесных уровней. С повышением температуры растет концентрация примесных носителей, значит растет и примесная проводимость. При достижении т. А (см. рис. 10.3,б; кривая 1) – температуры истощения примеси Т_S1 – все примесные носители будут переведены в зону проводимости.

Выше температуры Т_S1 и до температуры перехода к собственной проводимости Т_i1 (см. т. В, кривая 1, рис. 10.3,б) электропроводность падает, а сопротивление полупроводника растет. Выше температуры Т_i1 преобладает собственная электропроводность, т.е. в зону проводимости вследствие теплового возбуждения переходят собственные носители заряда. В области собственной проводимости σ растет, а ρ падает.

Для сильнолегированных полупроводников, у которых концентрация примеси n ~ 10²⁶ м^–3, т.е. соизмерима с концентрацией носителей заряда в металлах (см. кривая 3, рис. 10.3,б), зависимость σ от температуры наблюдается только в области собственной проводимости. С ростом концентрации примесей величина интервала АВ (АВ > A'B' > A"B") уменьшается (см. рис. 10.3,б).

Как в области примесной проводимости, так и в области собственной проводимости преобладает электрон-фононный механизм рассеяния. В области истощения примеси (интервалы AB, A'B', A"B") вблизи температуры Т_S преобладает электрон-примесное рассеяние. По мере увеличения температуры (перехода к Т_i) начинает преобладать электрон-фононное рассеяние. Таким образом, интервал АВ (A'B' или A"B"), называемый областью истощения примеси, является также областью перехода от механизма примесной проводимости к механизму собственной проводимости.