Л/Р: Тепловое расширение твердых тел

14.1. Цель работы

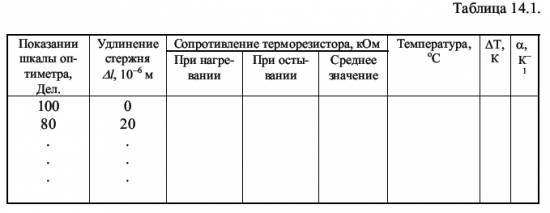
Определение температурного коэффициента линейного расширения металлического стержня в некотором интервале температур.

14.2. Содержание работы

Тепловое расширение – это изменение размеров тела в процессе его нагревания при постоянном давлении.

Причины теплового расширения можно понять, рассматривая классический осциллятор с учетом ангармоничности его колебаний.

Ангармоничность колебаний частиц твердого тела обусловлена характером зависимости сил взаимодействия между атомами от расстояния между ними.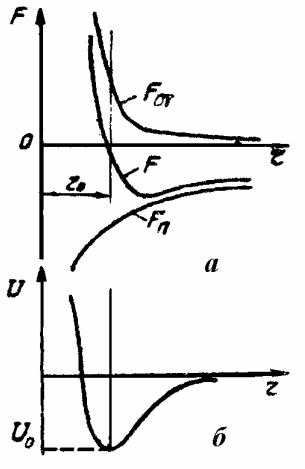

Независимо от природы сил, возникающих при сближении частиц (атомов или молекул), общий характер их остается одинаковым (рис. 14.1 а) [1]: на относительно больших расстояниях появляются силы притяжения F_n  , быстро увеличивающиеся с уменьшением расстояния r между частицами; на малых расстояниях возникают силы отталкивания F_от , которые с уменьшением r увеличиваются значительно быстрее, чем F_n.

На расстоянии r = r_o силы отталкивания уравновешивают силы притяжения и результирующая сила взаимодействия F обращается в нуль, а энергия взаимодействия достигает минимального значения U_o (рис. 14.1 б). Эти расстояния r_o определяют размер тела при абсолютном нуле температуры.

С повышением температуры частицы начинают колебаться около положений равновесия. Допустим частица 1 (рис. 14.2) закреплена неподвижно и колеблется лишь частица 2 вдоль оси х. Колеблющаяся частица обладает кинетической энергией, достигающей наибольшего значения E_к в момент прохождения положения равновесия О. На рис. 14.2 энергия E_к отложена вверх от дна потенциальной ямы авс.

При движении частицы 2 влево от положения равновесия кинетическая энергия расходуется на преодоление сил отталкивания ее от частицы 1 и переходит в потенциальную энергию взаимодействия частицы. Отклонение влево происходит до тех пор, пока вся кинетическая энергия частиц E_к не перейдет в потенциальную, которая увеличивается до U₁ =E_к , а частица 2 сместится предельно влево на расстояние х1.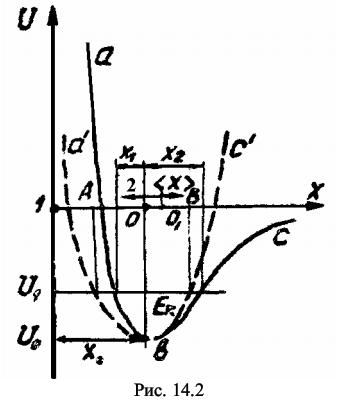

При движении частицы 2 вправо от положения равновесия кинетическая энергия расходуется на преодоление сил притяжения ее к частице 1 и также переходит в потенциальную энергию взаимодействия частиц. На расстоянии х2 от положения равновесия вся кинетическая энергия E_к переходит в потенциальную.




Если бы частица 2 совершала гармонические колебания, то сила, возникающая при смещении х частицы из положения равновесия, удовлетворяла бы закону Гука
а изменение потенциальной энергии U(х)

описывалось бы симметричной параболой а′ в с′ (см. рис. 14.2). Потому отклонения х₁ и х₂ были бы одинаковыми по величине и середина размаха АВ совпала бы с положением равновесия О. Нагревание тела в этом случае не могло бы вызвать его расширения, так как с увеличением температуры происходило бы лишь увеличение амплитуды колебаний частицы, а средние расстояния между ними оставались бы неизменными.

При х > 0 член ( g · x³ ) / 3 вычитается, а при х < 0, он прибавляется к (k · x²) /2,
что приводит к асимметрии потенциальной кривой.

Несимметричный характер потенциальной кривой приводит к тому, что отклонения частицы 2 вправо и влево оказываются неодинаковыми: вправо частица отклоняется сильнее, чем влево (см. рис. 14.2).

Вследствие этого среднее положение частицы 2 (точка О₁) уже не совпадает с положением равновесия О, а смещается вправо. Это соответствует увеличению среднего расстояния между частицами на <х>.

Таким образом, причиной теплового расширения тел является ангармонический характер колебаний частиц твердого тела, обусловленный ассиметрией кривой зависимости энергии взаимодействия частиц от расстояния между ними.

Количественно тепловое расширение твердых тел характеризуется температурным коэффициентом линейного расширения α, который показывает, на какую долю первоначальной длины l изменяются размеры тела при нагревании его на один градус, и определяется соотношением

Коэффициент α зависит от природы T твердых тел и вследствие анизотропии кристаллов может быть различным в различных направлениях. Коэффициент линейного расширения α в области низких температур зависит также от температуры: вблизи абсолютного нуля коэффициент α уменьшается с понижением температуры пропорционально кубу температуры, стремясь к нулю при абсолютном нуле.В области высоких температур для большинства материалов коэффициент линейного расширения практически не зависит от температуры, и тогда длина твердого тела возрастает линейно с температурой, а коэффициент α определяется выражением:


где l - длина тела при некоторой начально ∆T температуре Т₁;
∆l   -   удлинение   тела   при   нагревании   его   от   температуры   Т₁   до   Т₂ (∆Т = Т₂ - Т ₁).

По формуле (14.5) и определяют температурный коэффициент линейного расширения металлического стержня в данной работе.

14.3. Описание лабораторной установки

Исследуемый стержень 1 вместе с цилиндрическим нагревателем (рис. 14.3) помещен на столике 2 горизонтального оптиметра между контактными измерительными наконечниками 3 и 4, надеваемыми на штифты трубки оптиметра и пиноли 6.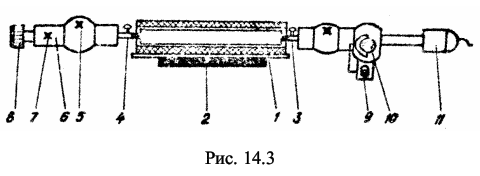




14.4. Методика проведения эксперимента и обработка результатов
14.4.1. Методика эксперимента

Для определения температурного коэффициента линейного расширения по формуле (14.5) необходимо измерить длину стержня l при некоторой температуре (например, комнатной), определить удлинение его при нагревании и соответствующее этому удлинению изменение температуры.

Удлинение стержня определяется по шкале оптиметра. Видимое в окуляр смещение шкалы на одно деление соответствует перемещению измерительного контакта (шрифта) 3, а следовательно, удлинению стержня на 1 мкм.

Температура стержня при нагревании определяется по сопротивлению терморезистора (активного полупроводникового элемента, электрическое сопротивление которого зависит от температуры). При нагревании сопротивление R терморезистора уменьшается. График зависимости R(T) для используемого в работе терморезистора приведен на лабораторном столе. Измерив сопротивление R терморезистора, по этому графику можно определить температуру стержня при любом его удлинении.

14.4.2. Порядок выполнения работы

1. Установите ручку трансформатора нагревателя на деление «нуль», затем включите осветитель прибора в сеть.
   
2. Отпустите винты 5 и 7 (см. рис. 14.3) и перемещая столик 2 и пиноль 6, установите их так, чтобы наконечники 3 и 4 касались с обоих концов стержня, а в поле зрения окуляра 9 появилась шкала. Винтом 5 закрепите пиноль 6.
   
3. Зеркальцем 10 добейтесь хорошей освещенности шкалы в поле зрения окуляра 9.
   
4. Вращая винт 8 пиноли, установите правый край шкалы (деление + 100) против указателя. Закрепите пиноль винтом 7.
   
5. Ознакомьтесь с измерителем сопротивления и подготовьте его к работе (инструкция на лабораторном столе).
   
6. Измерьте сопротивление R терморезистора при комнатной температуре, занесите результат в таблицу, при этом ∆ l = 0.
7. Включите нагреватель, для чего установите ручку трансформатора на де-ление «40 В», предварительно включив трансформатор в сеть.
   
8. Проводите измерения сопротивления R терморезистора через каждые 20 мкм удлинения стержня (20 делений шкалы) до общего удлинения       – 200 мкм. Данные заносите в таблицу.
   
9. Отключите нагреватель и проведите измерения сопротивления терморезистора при остывании стержня также через каждые 20 мкм.
   
10. Отключите установку.

14.4.3. Обработка результатов измерений

1. Для каждого удлинения вычислите среднее значение сопротивления терморезистора.
2. По средним значениям сопротивления определите температуру стержня, пользуясь графикомзависимости R(Т) терморезистора. Определите приращения температуры ∆Т, соответствующие каждому удлинению.
3. Изобразите графически зависимость ∆l = ƒ(∆Т). Через экспериментальные точки проведите прямую так, чтобы она лежала ближе к точкам и чтобы по об стороны ее оказалось приблизительно равное их количество.
4. Из графика определите отношение ∆l / ∆T, подставьте найденное значение в формулу (14.5) и определите температурный коэффициент линейного расширения стержня. Длина стержня приведена на лабораторном столе.
5. По значению α определите материал, из которого изготовлен стержень (смотрите таблицу на лабораторном столе).

1. Каков характер взаимодействия между атомами в твердых телах? Как силы взаимодействия атомов зависят от расстояния между ними?
2. Как объяснить тепловое расширение твердых тел?
3. Каков физический смысл температурного коэффициента линейного расширения?
4. Назовите размерность коэффициента линейного расширения в СИ.
5. Как определяется в работе температура стержня?
6. Перечислите основные источники погрешности определения α
   
7.