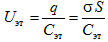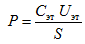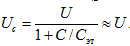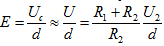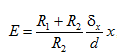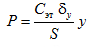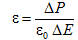Л/Р: Изучение диэлектрического гистерезиса сегнетоэлектриков
Цели работы:
Методическое обоснование работыДиэлектрики – вещества, не способные проводить электрический ток. Диэлектрики бывают твердые, жидкие и газообразные. Твердые диэлектрики – это прежде всего аморфные вещества, т.е. вещества, не имеющие кристаллической структуры. К ним относятся многие пластмассы, стекло, воск и др. Аморфные вещества изотропны (обладают свойствами, одинаковыми по всем направлениям). Кристаллические диэлектрики отличаются от аморфных наличием анизотропии, что определяется периодическим строением их кристаллической решетки и при-водит к тому, что различные физические свойства, например, электрические, оптические, тепловые и др. в таких веществах сильно зависят от направления в кристалле. Способность диэлектриков поляризоваться – одно из их фундаментальных свойств. Физические механизмы поляризации могут быть разными.
Следует подчеркнуть, что во всех указанных случаях поляризация приводит к возникновению макроскопического электрического момента, а диэлектрик оказывается поляризованным в целом. В качестве величины, характеризующей степень поляризации, используется вектор поляризации Ṗ (называемый также поляризованностью), представляющий собой электрический дипольный момент единицы объема вещества:
(2.3.1) Следует подчеркнуть, что во всех указанных случаях поляризация приводит к возникновению макроскопического электрического момента, а диэлектрик оказывается поляризованным в целом. В качестве величины, характеризующей степень поляризации, используется вектор поляризации где – дипольный момент молекулы; – физически бесконечно малый объем; N – количество молекул в этом объеме. Для изотропных диэлектриков вектор поляризации Ṗ связан с напряженностью внешнего электрического поля соотношением:
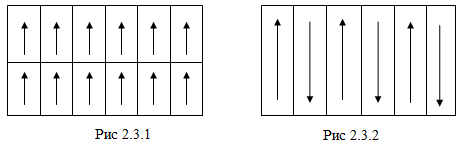
(2.3.2) где ᵡ - диэлектрическая восприимчивость, не зависящая от Ē, ε0- электрическая постоянная, равная 8,85 * 10 -12 Ф/м. Соотношение значительно усложняется при переходе к анизотропным диэлектрикам (кристаллам), так как в этом случае ᵡ не является скалярной величиной. Диэлектрическая восприимчивость в анизотропном кристалле зависит от того, в каком направлении исследуются его свойства, т.е. ᵡ является тензором. В некоторых ионных кристаллах поляризация может возникать и существовать самопроизвольно (спонтанно) в отсутствие внешнего электрического поля. Известны два типа нелинейных диэлектриков, обладающих спонтанной поляризацией: пироэлектрики и сегнетоэлектрики. В пироэлектриках электрические диполи всех элементарных ячеек кристалла ориентированы в одном направлении. Совокупности спонтанно поляризованных ячеек образуют области, называемые доменами. В сегнетоэлектриках в пределах каждого домена все диполи элементарных ячеек ориентированы одинаково, в то время как сами домены могут быть ориентированы по-разному (рис. 2.3.2). Размеры доменов различны как для разных сегнетоэлектриков, так и для одного и того же кристалла. Они могут быть как очень малыми (~10-6), так и достигать в длину нескольких сантиметров.
Сегнетоэлектричество. Разбиение сегнетоэлектриков на домены обусловливает ряд его нелинейных свойств и в первую очередь нелинейную зависимость электрической поляризации Ṗ от величины внешнего электрического поля Ē:
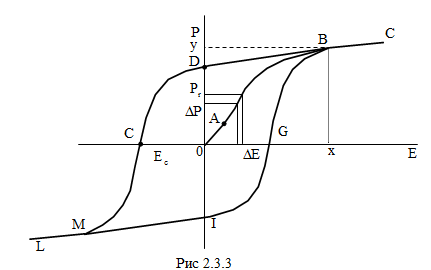
(2.3.3) Эта зависимость объясняется тем, что направление в доменах сегнетоэлектриков может быть изменено внешним электрическим полем. У пироэлектриков никаким внешним полем невозможно изменить ориентацию доменов и соответственно направление вектора спонтанной поляризованности . Таким образом, сегнетоэлектрики – это вещества, у которых спонтанная поляризация может менять свое направление под действием внешнего электрического поля. Кроме того, для сегнетоэлектриков существует определенная температурная область существования доменов, т.е. сегнетоэлектрического состояния. Для каждого конкретного сегнетоэлектрика существует определенная температура, которая называется температурой Кюри (Tc), ниже которой он обладает сегнетоэлектрическими свойствами, а выше – ведет себя как обычный линейный диэлектрик. Нелинейная зависимость поляризации от внешнего поля, свойственная сегнетоэлектрикам, приводит в переменных электрических полях к диэлектрическому гистерезису (рис. 2.3.3). Рассмотрение петель гистерезиса позволяет получить наглядное представление о роли доменов в поляризации сегнетоэлектрика.
Схематично это представление сводится к следующему. В слабых полях (рис. 2.3.3, участок OA) поляризация P еще линейно зависит от поля, т.е. соотношение (2.3.2), где , справедливо, и домены к процессу переполяризации не подключаются. На участке АВ наблюдается эффективный рост поляризации, что связано в основном с нелинейным процессом переориентации доменов вдоль направления внешнего электрического поля. В точке В все домены ориентированы по внешнему полю и дальнейшее возрастание P (опять линейное) по мере увеличения Ē не связано с доменной структурой и характеризует индуцированную полем поляризацию (участок BC). Состояние образца от точки B и выше называется монодоменным, а схематично он стал похож на пироэлектрик (рис. 2.3.1). Уменьшение величины поля Ē, начиная с точки B, повторяет (в обратном порядке) процесс первичной поляризации; при уменьшении поля до нуля поляризация не обращается в нуль, а величина ее Pr, носит название остаточной поляризации. Наличие этой поляризации свидетельствует о том, что кристалл в отсутствие внешнего поля (Ē = 0) "пытается сохранить" свое монодоменное состояние (ориентацию всех доменов в одном направлении). Приложение поля в обратном направлении приводит к уменьшений поляризации и при напряженности поля Eс, поляризация становится равной нулю. Такое поле называется коэрцитивным. Таким образом, при полях, близких к коэрцитивным, происходит интенсивная переполяризация доменов – изменение знака их поляризации на противоположное. Дальнейшее повышение значений поля приводит к насыщению (участок МL), т.е. к ориентации всех доменов в одном направлении, только противоположном по сравнению с участком ВС. Уменьшение значений напряженности электрического поля от значения, соответствующего точке L, повторяет процесс, рассмотренный на участке ВD. В точке В гистерезисный цикл заканчивается. При следующем периоде изменения поля процесс переполяризации снова идет по рассмотренному циклу. Петли диэлектрического гистерезиса, изучаемые в данной работе на образцах сегнетоэлектрика триглицинсульфата (ТГС), отличаются высокой прямоугольностью. Нелинейная связь между поляризацией и напряженностью электрического поля есть одна из основных и определяющих характеристик сегнетоэлектрика (рис. 2.3.4, а). Ответственной за эту нелинейность, как указывалось выше, является доменная структура. Диэлектрическая проницаемость сегнетоэлектрика может быть определена из зависимости на основании следующего выражения:
Так как для большинства сегнетоэлектриков значения ε >> 1, получим:
(2.3.4)
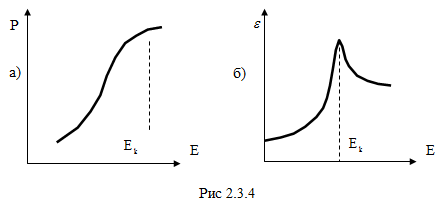
Учитывая справедливость (2.3.4), можем утверждать, что вид зависимости (рис. 2.3.4, а) определяет характер поведения диэлектрической проницаемости ε
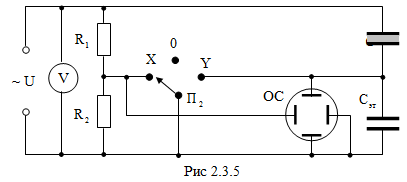
= ε (E) (рис. 2.3.4, б). При этом диэлектрическая проницаемость достигает своего максимального значения при напряженности электрического поля Ek, соответствующей точке перегиба на кривой. Схема лабораторной установки приведена на рис. 2.3.5.
На вход "X" осциллографа (ОС) подается напряжение с сопротивления R2, а на вход "Y" – с эталонного конденсатора Сэт. Для удобства измерений в схему введен переключатель (П2), позволяющий проектировать петлю гистерезиса на оси "X" или "Y". При замыкании П2 на "X" закорачивается вход "X" осциллографа и петля на экране осциллографа вырождается в вертикальную прямую, а при замыкании на "Y" – в горизонтальную прямую. На горизонтальные пластины осциллографа подается напряжение U2 пропорциональное входному напряжению U
(2.3.5) Два последовательно соединенных конденсатора С и Сэт включены параллельно делителю напряжения R1 и R2. Так как заряды на конденсаторах С и Сэт одинаковы, то
где Uэт – напряжение на эталонном конденсаторе; Uc – напряжение на образце.Учитывая равенство зарядов на конденсаторах, получим
(2.3.6) где S – площадь пластины конденсатора C. Так как P ≈ σ , то из (2.3.6) следует
(2.3.7) Поскольку Сэт >> С, то
Используя формулу связи напряженности E с разностью потенциалов Uс, получим
(2.3.8) где d – расстояние между пластинами конденсатора C; U2 – напряжение, подаваемое на вход "X" осциллографа. Расчет E, P и ε производится по рабочим формулам
(2.3.9)
(2.3.10)
(2.3.11)
где d и S – толщина и площадь исследуемого образца; δx и δy – чувствительность осциллографа по осям "X" и "У" соответственно; x и y – координаты вершины петли гистерезиса. Задание
Контрольные вопросы
Литература
© Министерство образования Республики Беларусь, Белорусский Государственный Университет Информатики и Радиоэлектроники, Кафедра физики Добавил: sidius1713 (31.01.2012) | Категория: Электричество (не ВолгГТУ) Просмотров: 10616 | Загрузок: 0 | Рейтинг: 5.0/1 | Теги: | |||||||||||||||||||||||||||||
| Комментарии (0) | |

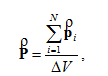
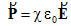
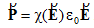
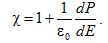
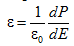
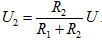
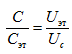 ,
,