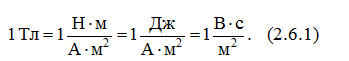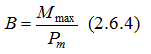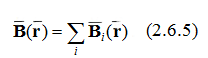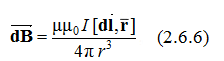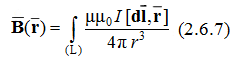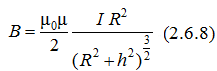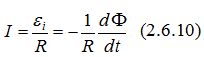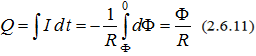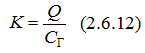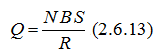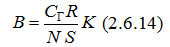Изучение магнитных полей - лабораторная работа

Цели работы

1. Ознакомиться с одним из методов измерения индукции магнитного поля.
   
2. Изучить магнитное поле тока катушки.
   
3. Проверить справедливость принципа суперпозиции магнитных полей.
   

Магнитное поле – это силовое поле, действующее на движущиеся электрические заряды, проводники с током и на тела, обладающие магнитным моментом (независимо от состояния их движения). Эти же объекты являются источниками магнитных полей.

Так, например, магнитное поле создается токами в электролитах, электрическими разрядами в газах, катодными и анодными лучами, проявляется при движении электронов в атомах, при колебаниях атомных ядер в молекулах, при изменении ориентации элементарных диполей в диэлектриках и т.д. Природа этих источников едина; магнитное поле возникает в результате движения заряженных микрочастиц (электронов, протонов, ионов), а также благодаря наличию у микрочастиц собственного (спинового) магнитного момента.

Силовой характеристикой магнитного поля является магнитная индукция Ḃ. Значение Ḃ определяет силу, действующую в данной точке поля на движущийся электрический заряд, проводник с током или на тело, обладающее магнитным моментом Ṗ_m. В СИ единица магнитной индукции получила название тесла (Тл):

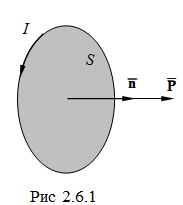
Магнитного аналога электрическому заряду в природе не существует. Пробным телом, пригодным для определения и измерения магнитного поля, может быть элементарный контур с током, магнитным полем которого можно пренебречь.

Количественной характеристикой контура с током  I  является его магнитный момент Ṗ_m:

Ṗ_m = I S ṅ

(2.6.2.)

где S – площадь поверхности, ограниченной контуром L; ṅ – единичный вектор нормали к этой поверхности.

Направление тока и нормали к поверхности образуют правовинтовую систему (рис.2.6.1).

На плоский контур с током, помещенный в однородное магнитное поле, действует, момент сил:

В положении устойчивого равновесия контура Ṗ↑↑ Ḃ. Модуль момента сил M = Ṗ_m B sin(ṅḂ).

Соотношение (2.6.3) можно рассматривать как:

где M_max – максимальный момент сил, действующий на контур с током. Направление вектора определяется направлением магнитного момента в равновесном положении контура.

Основной задачей теории магнитного поля является расчет характеристик магнитного поля произвольной системы токов и движущихся электрических зарядов. В основе метода расчета магнитных полей лежит принцип суперпозиции: магнитное поле, порождаемое несколькими движущимися зарядами (токами) в данной точке пространства, равно векторной сумме магнитных полей, порождаемых каждым зарядом (током) в этой точке в отдельности.

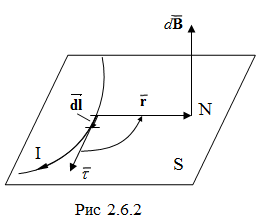
Согласно закону Био-Савара-Лапласа, элемент проводника, вектор dl (рис.2.6.2), по которому идет ток I создает в точке N, находящейся на расстоянии вектора r от вектора dl, магнитное поле

где μ₀ – магнитная постоянная (μ₀ = 1,26*10^-6 Гн/м); μ – магнитная проницаемость среды.

Элемент вектор dl направлен по касательной к вектору τ проводнику по току.

Вектор Ḃ (r) перпендикулярен плоскости S, содержащей векторы и (рис. 2.6.2). Направление совпадает с поступательным движением правого буравчика при вращении его рукоятки в плоскости S от вектора dl к вектору r по кратчайшему пути. Магнитное поле, создаваемое линейным проводником L с током I, описывается вектором магнитной индукции:

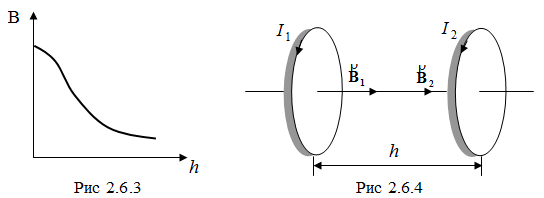
где интегрирование производится по всей длине проводника L.

Применяя закон Био-Савара-Лапласа и принцип суперпозиции, можно рассчитать индукцию магнитного поля, создаваемого токами различных конфигураций.

В частности, магнитное поле, создаваемое кольцевым проводником с током I в произвольной точке, лежащей на оси проводника на расстоянии h от его плоскости

Зависимость индукции B от расстояния h изображена на рис. 2.6.3.

В работе исследуются магнитные поля двух соосных катушек, расположенных на расстоянии h друг от друга, по виткам которых идут токи одного направления (рис. 2.6.4). Индукция магнитного поля в любой точке на оси катушек равна векторной сумме индукций, создаваемых этими катушками по отдельности в той же точке

Для измерения индукции магнитного поля в работе применяется баллистический гальванометр. Метод измерения величины магнитной индукции основан на явлении электромагнитной индукции – возникновении ЭДС индукции в измерительной катушке при изменении магнитного потока Ф через поверхность, ограниченную витками катушки.

Измерительную катушку располагают так, чтобы вектор Ḃ (r)  оказался перпендикулярным к плоскости ее витков. Величина магнитной индукции B определяется по измерению магнитного потока через поперечное сечение измерительной катушки при выключении тока I, создающего поле.

Вследствие этого в катушке наводится ЭДС индукции ε_i, которая создает импульс тока

где R – полное сопротивление цепи.

Этот ток за время t перенесет через измерительную цепь заряд

и отбросит "зайчик" гальванометра на K делений

где C_г– цена деления баллистического гальванометра.

Так как полный магнитный поток через поперечное сечение катушки Ф = BSN, где S – площадь витка, в пределах которого поле можно считать однородным, N – число витков катушки, то согласно формуле (2.6.11), по цепи пройдет заряд

Измеряя максимальное отклонение "зайчика" гальванометра и зная постоянную прибора , можно вычислить магнитную индукцию по формуле

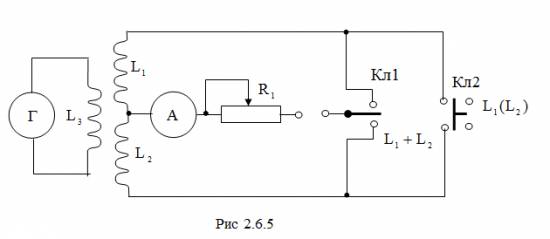
Принципиальная схема установки изображена на рис.2.6.5. Исследуемые поля катушек L₁ и L₂, создаются постоянным током. Заряд Q измеряется баллистическим гальванометром (Г). Измерительная катушка L₃ жестко насажена на стержень, с помощью которого может перемещаться вдоль осей катушек L₁ и L₂. Полное сопротивление измерительной цепи R равно сумме сопротивлений катушки L₃, соединенных проводов и баллистического гальванометра. Ток в катушках L₁ и L₂ изменяется потенциометром R₁.

Задание

1. Для каждой из катушек L₁и L₂измерить на их оси через каждый сантиметр максимальные отклонения K "зайчика" гальванометра при выключении тока, создающего поле.Рассчитать магнитную индукцию B на оси катушек по формуле (2.6.14). Данные измерений и расчетов занести в табл. 2.6.1.Построить зависимости B_L1 = B_L1 (l) и B_L2 = BL2 (l) в одной системе координат.
   
2. Проделать аналогичные измерения результирующего магнитного поля при одновременном протекании тока в катушках L₁и L₂ , при этом сила тока в каждой катушке должна быть такой же, как и в п. 1. Результаты измерений и расчетов магнитной индукции занести в табл. 2.6.1.Построить зависимости B_р = B_р (l) и B(l) = B_L1 (l) + B_L2 (l) в одной системе координат.
   
3. Провести анализ полученных результатов.
   
4. С помощью программы MathCad теоретически рассчитать индукцию магнитного поля, создаваемого токами в катушках L₁ и L₂, на их оси. Проанализировать экспериментальные и теоретические зависимости.

Контрольные вопросы

1. Дать определение магнитного поля. Назвать его источники. Сформулировать принцип суперпозиции магнитных полей.
   
2. Записать закон Био-Савара-Лапласа. Как определить направление вектора dB?
   
3. В чем состоит явление электромагнитной индукции? Определить направления индукционного тока в измерительной катушке при включении и выключении тока в катушке, создающей магнитное поле.
   
4. Перечислить все физические явления, лежащие в основе предложенного метода исследования магнитного поля катушек.
   
5. Пояснить принцип работы используемой схемы.
   
6. Используя закон Био-Савара-Лапласа и принцип суперпозиции магнитных полей, получить формулу (2.6.8).
   

Литуратура

• Савельев И.В. Курс общей физики. Электричество и магнетизм.–М.: Наука, 1982, Т.2.