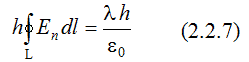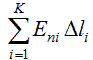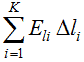Л/Р: Изучение основных свойств электростатического поля
| [Скачать с сервера (35.7 Kb) - бесплатно] | 17.12.2011, 23:39 |
Цель работы
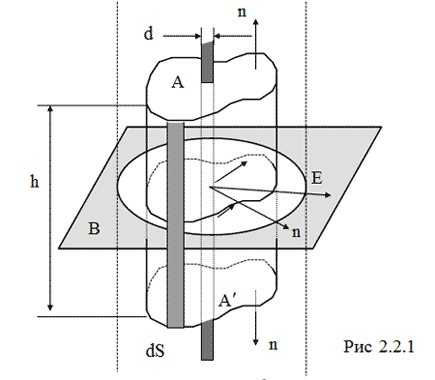
Методическое обоснование работыИзучать свойства электростатистического поля особенно удобно на примере плоского поля, т.е. поля, в котором векторы E лежат в параллельных плоскостях, а потенциал и напряженность зависят только от двух координат. Полное исследование такого поля требует измерений потенциала или напряженности только в одной из плоскостей. В качестве примера плоского поля в работе выбрано поле, являющееся аналогом электростатического поля бесконечного цилиндрического конденсатора, внешняя обкладка которого обозначена С1, а внутренняя – С2 (рис. 2.2.1). Теорема Гаусса утверждает, что поток Ф вектора напряженности электрического поля E через любую замкнутую поверхность S равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на ε0: 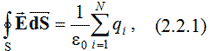 где 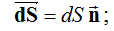 Вектор n – единичный вектор внешней нормали к поверхности;
В случае бесконечного цилиндрического конденсатора при применении теоремы Гаусса в качестве вспомогательной поверхности целесообразно выбрать замкнутую цилиндрическую поверхность S, площадь которой S = S1 + S2 + S3 (2.2.2) где S1, S2 – площади торцов; S3 – площадь боковой поверхности. Высота h цилиндра, ограниченного вспомогательной (гауссовой) поверхностью выбирается произвольно; при этом она обязательно должна быть конечной. Гауссова поверхность охватывает заряд q, локализованный на участке AA' (рис. 2.2.1) внутренней обкладки конденсатора длиной h. Поток вектора E через выбранную замкнутую поверхность равен сумме потоков через боковую поверхность и торцы: 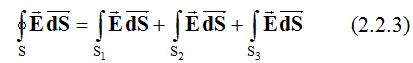 Поскольку во всех точках торцов векторы E и n взаимно перпендикулярны, то потоки вектора E через эти поверхности равны нулю, т.е. 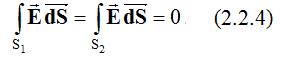 Таким образом: 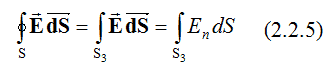 где En – проекция вектора E на направление внешней нормали n; Учитывая, что диаметр внутренней обкладки конденсатора d << D (D – диаметр внешней обкладки), внутреннюю обкладку конденсатора можно представить в виде бесконечно длинной нити, заряженный с линейной плотностью ?. Тогда заряд q, локализованный внутри гауссовой поверхности, равен q = λh (2.2.6) С учетом соотношений (2.2.3) – (2.2.6), выражение (2.2.1) может быть приведено к виду:
откуда 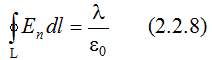 где интегрирование производится по замкнутому контуру L, представляющему собой плоский аналог гауссовой поверхности. Полученный результат не зависит от координаты Z и справедлив для любого контура L, лежащего в плоскости ХY. Интеграл 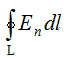 приближенно можно представить в виде суммы 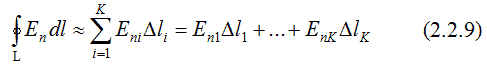 Таким образом, в соответствии с теоремой Гаусса для поля вектора E 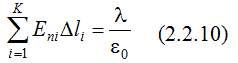 Необходимо отметить, что 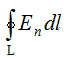 или 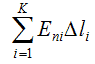 (линейный поток вектора E) в этом случае является аналогом потока вектора E через замкнутую поверхность, λ – аналогом заряда. Условием потенциальности векторного поля является равенство нулю циркуляции вектора напряженности этого поля по любому замкнутому контуру. Потенциальность исследуемого поля математически может быть охарактеризована выражением 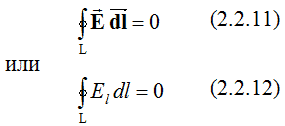 где El – проекция вектора напряженности на направление элементарного перемещения dl вдоль контура L в данной точке поля; 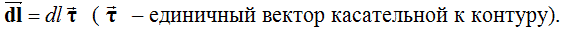 Выражения (2.2.11), (2.2.12) являются математической формулировкой теоремы о циркуляции вектора E. Левую часть (2.2.12) можно представить в виде суммы 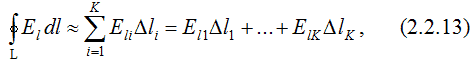 где Eli – тангенциальная составляющая вектора E в пределах участка контура Δli. Таким образом, теорема о циркуляции поля вектора E может быть записана в виде 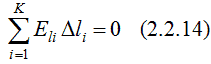 Используемый в лабораторной работе макет (рис. 2.2.2) является плоским аналогом рассмотренного цилиндрического конденсатора. Метод моделирования эквивалентных полей подробно рассмотрен в описании к предшествующей лабораторной работе - "Изучение строения электростатических полей". Макет представляет собой лист электропроводной бумаги, на которой закреплены плоские металлические электроды, подсоединенные к истопнику постоянного тока. Разность потенциалов между двумя произвольными точками поля измеряем с помощью двойного зонда (ДЗ), соединенного с цифровым вольтметром (или другим измерительным прибором). Измеряемая разность потенциалов однозначно связана с напряженностью поля в пределах участка Δl. 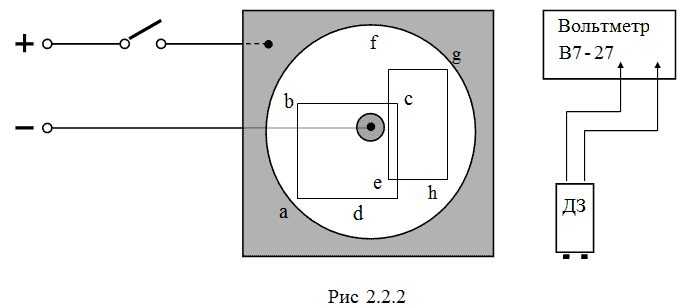
Зонд (ДЗ) необходимо расположить таким образом, чтобы его центр совпадал с центром каждого участка Δli. При проверке теоремы Гаусса стрелка зонда должна быть ориентирована по направлению внешней нормали к контуру (рис. 2.2.3); при проверке равенства нулю циркуляции вектора E – по касательной к контуру в направлении его обхода, которое выбирается произвольно (рис. 2.2.4). 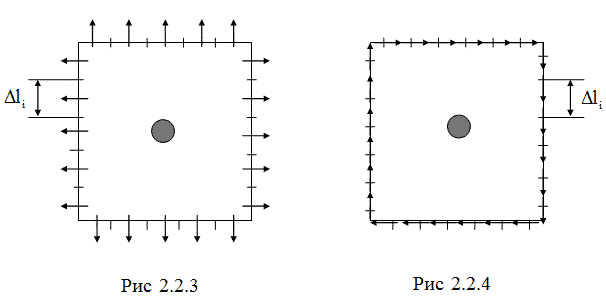 Задание
Контрольные вопросы
Литература
© Министерство образования Республики Беларусь, Белорусский Государственный Университет Информатики и Радиоэлектроники, Кафедра физики Добавил: mauzer (17.12.2011) | Категория: Электричество (не ВолгГТУ) Просмотров: 4806 | Загрузок: 1208 | Рейтинг: 5.0/1 | Теги: | |
| Комментарии (0) | |