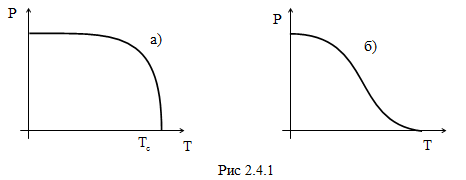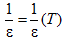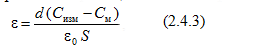Л/Р: Изучение температурной зависимости диэлектрической проницаемости сегнетоэлектриков вблизи температуры фазового перехода

Цели работы

• Изучить поведение диэлектрической проницаемости сегнетоэлектриков вблизи температуры фазового перехода.
  
• Определить постоянную Кюри-Вейсса и тип фазового перехода.

Методическое обоснование работы

Фазовые переходы (ФП) наблюдаются для многих веществ при определенной температуре. Типичным примером фазового перехода первого рода является таяние льда при Т = 0° C, плавление металлов при высоких температурах, кипение воды и др. Переходы в твердом теле между различными фазами вещества, обладающими разными физическими свойствами, очевидно должны происходить с перестройкой кристаллической структуры. Если такая перестройка в твердом теле (при определенной температуре) происходит скачком, то говорят, что происходит фазовый переход первого рода.

Однако наряду с таким скачкообразным изменением состояния кристаллической решетки возможен и другой тип перестройки структуры – непрерывный. Непрерывный переход из одной кристаллической модификации (с определенным расположением атомов) в другую (с другим расположением) называется фазовым переходом второго рода.

В качестве примера ФП второго рода можно привести переход металла в сверхпроводящее состояние при низкой температуре и переход жидкого гелия в сверхтекучее состояние. В обоих случаях состояние тела меняется непрерывным образом в некотором температурном интервале, но в точке фазового перехода тело приобретает качественно новые свойства.

Фазовые переходы второго рода чаще всего встречаются в полярных диэлектриках, например, сегнетоэлектриках. Сегнетоэлектрики – кристаллические вещества, у которых спонтанная поляризация может менять свое направлений под действием внешнего электрического поля. Характерной особенностью сегнетоэлектрических кристаллов является возникновение спонтанной поляризации Р при уменьшении температуры вещества ниже некоторой температуры T_c.

Эта температура называется точкой Кюри. В точке Кюри поляризация Р еще равна нулю, однако, сколь угодно малое понижение температуры приводит к переходу кристалла в новую – сегнетоэлектрическую – фазу с другим порядком в расположении атомов в узлах кристаллической решетки и возникновени-ем доменной структуры. Точка Кюри – это температура фазового перехода. Если при понижении температуры реализуется фазовый переход первого рода, то поляризация возникает скачком, если второго – то поляризация возникает и плавно растет при дальнейшем понижении температуры (рис. 2.4.1).

• а) – фазовый переход первого рода;
  
• б) – фазовый переход второго рода.
  

Различие в поведении P_c = P_c(T) для обоих типов ФП определяет и различие в температурных зависимостях других физических параметров сегнетоэлектриков, особенно вблизи точки Кюри.

Современная техника требует много различных электрических кристаллов. Одни кристаллы преобразуют тепло в электричество и наоборот. Это пироэлектрики. Таковы, например, турмалин, сахар и др. Другие кристаллы – пьезоэлектрики – деформируются под действием электрического поля, а механические нагрузки вызывают в них электрическую поляризацию. Наиболее известный пьезоэлектрический кристалл – кварц. Кристаллы пьезоэлектриков излучают и принимают звук и ультразвук, стабилизируют по частоте излучение радиостанций, разграничивают частотные диапазоны в высокочастотной телефонии, служат активными элементами в измерительных приборах. Квантовая радиоэлектроника также не обходится без электрических кристаллов. Такие кристаллы управляют лазерным пучком: отклоняют его, модулируют по интенсивности, обеспечивают получение мощных ("гигантских") импульсов.

Среди электрических кристаллов центральное место принадлежит сегнетоэлектрикам. Такими кристаллами являются сегнетовая соль, титанат бария, дигидрофосфат калия, триглицинсульфат (ТГС) и др. Сегнетоэлектрики имеют высокую диклектрическую проницаемость, что позволяет делать малогабаритные конденсаторы большой емкости.

В окрестности точки Кюри сегнетоэлектрики испытывают аномалии практически всех физических свойств: тепловых, механических, электрических, оптических. Природа этих аномалий ещё не до конца понята, но резкое изменение свойств сегнетоэлектриков может быть выгодно использовано и уже используется в измерительной аппаратуре и радиоаппаратуре.

Под пироэлектрическим эффектом понимают процесс изменения спонтанной поляризации при изменении температуры, т.е. способность некоторых кристаллов поляризоваться при нагревании. Суть этой поляризации сводится к появлению с одной стороны однородного кристаллического образца отрицательного, а с противоположной – положительного заряда при изменении температуры. В сегнетоэлектрических кристаллах спонтанная поляризация, а значит, и величина поверхностной плотности заряда P_n = σ' сильно зависят от температуры, особенно вблизи точки Кюри. Это привело к использованию таких материалов в качестве чувствительных элементов пироприёмников инфракрасного излучения, а также для измерения различных характеристик лазеров и регистрации мощности СВЧ-сантиметрового и миллиметрового диапазонов. Кроме того, в настоящее время интенсивно ведутся разработки устройств, преобразующих тепловую энергию, например, энергию Солнца, в электрическую.

Значения диэлектрической проницаемости сегнетоэлектрических кристаллов велики, особенно при приближении кристалла к температуре фазового перехода. Большие значения ε традиционно связывают с подвижностью доменной структуры сегнетоэлектриков во внешнем электрическом поле. Температурная зависимость диэлектрической проницаемости выше точки Кюри Т_с описывается законом Кюри-Вейсса:

где С - постоянная Кюри; Тс – температура, при которой происходит фазовый переход, связанный с возникновением или исчезновением спонтанной поляризации.

Название Тс температурой Кюри дано по аналогии с ферромагнетиками. Фаза вещества при T < Tc называется сегнетоэлектрической, а при T > Tc – параэлектрической. В параэлектрической фазе кристалл ведет себя как обычный линейный диэлектрик, а значения диэлектрической проницаемости уже через несколько градусов выше точки Кюри становятся малыми (ε = 5 – 30). Из выражения (2.4.1) видно, что при T →Tc диэлектрическая проницаемость ε → ∞. Экспериментальные значения ε при T = Tc, полученные в слабых из-мерительных электрических полях, являются конечными (для ТГС такие значения ε ~ 6*10⁴).

Одним из важнейших параметров сегнетоэлектрика является постоянная Кюри-Вейсса C, характеризующая как тип, так и особенности фазового перехода. Если эта величина C ~10³, то фазовый переход в таком кристалле происходит с упорядочением некоторых структурных элементов: ионов, протонов и даже групп атомов. Такой фазовый переход называют переходом типа порядок-беспорядок. Если же постоянная С ~ 10⁵, то ФП является переходом типа смещения, который происходит в результате смещения одного или нескольких атомов относительно первоначального положения равновесия (положения равновесия в параэлектрической фазе).

Исходя из формулы (2.4.1) постоянная Кюри-Вейсса:

Постоянную Кюри-Вейсса удобно также определить с помощью графика зависимости

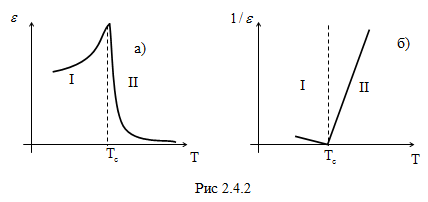
(рис. 2.4.2, б), так как в пределах ∆T = T - T_c ~ 15° (Т – температура параэлектрической фазы) зависимость носит линейный характер.

• I – сегнетоэлектрическая фаза ( T < T_c ); 
  
• П – параэлектрическая фаза ( T > T_c ).
  

В настоящей работе диэлектрическая проницаемость ε определяется для кристалла ТГС на основании измерения емкости конденсатора, между обкладками которого находится исследуемый образец. Образец для измерения изготовлен в форме прямоугольного параллелепипеда, толщина d которого намного меньше его длины. Измеряя емкость такого плоского конденсатора, можно определить значения диэлектрической проницаемости из выражения

где C_изм – измеряемая емкость; С_м – емкость монтажа; S – площадь образца; d – его толщина.

Изменяя температуру образца и измеряя значение емкости при этом, можно получить температурную зависимость ε в любом интервале температур, включая T_c (рис. 2.4.2, а).

Схема лабораторной установки включает измеритель емкости и термостат с исследуемым образцом (рис. 2.4.3).

Задание

1. Измерить емкость образца при различных температурах.
2. Вычислить значения диэлектрической проницаемости по формуле (2.4.3) для каждой температуры.
   
3. Результаты измерений и вычислений занести в таблицу.
4. По полученным данным построить графики зависимостей ε = ε(T) и
   
   
   
   
5. Использовав данные зависимости
   
   
   
   в параэлектрической фазе, определить значение постоянной Кюри-Вейсса из выражения (2.4.2).
6. По значению величины постоянной Кюри-Вейсса определить тип фазового перехода сегнетоэлектрика.

Контрольные вопросы

1. Что называется фазовым переходом?
   
2. Какие фазовые переходы могут происходить в твердых телах?
   
3. Какие структурные изменения происходят при фазовых переходах в сегнетоэлектриках?
   
4. Каковы значения диэлектрической проницаемости для сегнетоэлектрических кристаллов? Как зависит диэлектрическая проницаемость сегнетоэлек-триков от температуры?
   
5. Записать выражение для закона Кюри-Вейсса. Пояснить как из графика зависимости 1/ ε = f(T) определить постоянную Кюри-Вейсса? Что она характеризует?
   
6. Где применяется полярные диэлектрики?
   
7. Что понимают под пироэлектрическим эффектом?
   
8. В чем суть пьезоэлектрического эффекта?

Литература

1. Савельев И.В. Курс общей физики в 3-х т. Электричество и магнетизм. Волны и оптика. –М.; Наука. 1988. Т.2. §§ 15-19, 23; § 12-14, 17. 4-6.

© Министерство  образования Республики Беларусь, Белорусский Государственный Университет Информатики и Радиоэлектроники, Кафедра физики