Изучение спектрального прибора

3.1. Цель работы
Ознакомление с принципом действия и устройством спектрального прибора – монохроматора УМ-2, построение градуировочного графика монохроматора и определение его дисперсионных характеристик.



3.2. Содержание работы
В практике заводских лабораторий и научных исследований широкое распространение получили спектральные приборы для решения большинства спектрально-аналитических задач. Можно назвать некоторые из этих задач: быстрый контроль состава больших партий готовых деталей, которые после контроля идут для сборки изделий, экспрессный контроль состава пробы литейного цеха, определение состава незначительного включения на поверхности детали, контроль новых соединений, определение ничтожных концентраций микроэлементов в биофизике, агрофизике, агрохимии, медицине, биологии и т. д.

Спектральные приборы обеспечивают разложение идущего от источника излучения в спектр по длинам волн. Применяются два типа спектрального разложения: при преломлении света в призмах (призменные спектральные приборы) и при дифракции света в дифракционных решетках (дифракционные спектральные приборы).

Принципиальная оптическая схема призменного спектрального прибора представлена на рис. 3.1. Основными частями прибора являются:

• коллиматор, состоящий из щели 1 и объектива 2;
• диспергирующая призма 3;
• камерный объектив 4 или зрительная труба 4-5.

Коллиматор служит для получения параллельного пучка света, для чего щель 1 помещается в фокальной плоскости объектива коллиматора 2.

Параллельный пучок света падает на призму диспергирующей системы. Отклонение ϕ луча после прохождения призмы зависит от преломляющего угла α призмы и от её показателя преломления n и определяется следующей формулой (в случае наименьшего отклонения, т. е. в том ее положении, когда внутри призмы луч идет параллельно основанию):
Для многопризменных приборов угловая ширина Δϕ увеличивается в зависимости от числа призм K, и тогда

Лучи разных длин волн λ₁ и λ₂ не параллельны друг другу, но световой пучок, состоящий из лучей одной длины волны λ₁ (на рисунке заштрихован), или λ₂, остается строго параллельным. Такой пучок попадает в камерный объектив 4.

Камерный объектив 4 собирает эти параллельные пучки в своей фокальной поверхности ab. На экране, расположенном в фокальной плоскости камеры, наблюдаются изображения входной щели в монохроматическом свете, соответствующие различным длинам волн – спектральные линии. Совокупность спек-тральных линий составляет спектр. Если для наблюдения спектра устанавливается окуляр 5 (визуальное наблюдение), то прибор называется спектроскопом. Можно в фокальной плоскости ab установить фотопластинку и получить спектрограмму – фотографию спектра. Такой прибор носит название спектрографа.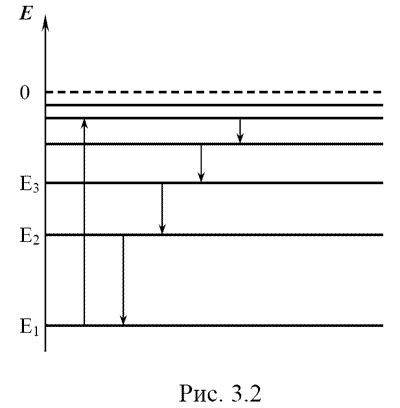


Основными характеристиками спектрального прибора являются угловая и линейная дисперсии.
Угловая дисперсия β определяется:

где dϕ – угол между направлениями лучей λ₁ и λ₂ = λ₁ + dλ (см. рис. 3.1).

Угловая дисперсия определяется по (3.3) дисперсией призмы dn / dλ, преломляющим углом α призмы и числом призм K.

Линейная дисперсия определяется расстоянием на фокальной плоскости ab, на которое разведены лучи с единичным интервалом длин волн, т.е. dl / dλ. Выражается линейная дисперсия в миллиметрах на нанометр (мм/нм). На практике обычно употребляют обратную величину dλ / dl, называемую обратной линейной дисперсией, определяющей значение интервала длин волн, приходящегося на 1 мм длины спектра.

По значению угловой дисперсии β можно определить линейную дисперсию

где f – фокусное расстояние камерного объектива.

В разных участках спектра угловая и линейная дисперсии призменных спектральных приборов имеют различные значения. Поэтому угловое и линейное расстояние между спектральными линиями, отличающимися по длине волны на одно и то же значение, будут также различными в разных участках спектра.





Тип спектра, получаемого с помощью спектрального прибора, зависит от используемого источника света S.

Если источником света S служит, например, лампа накаливания, то в фокальной плоскости наблюдается сплошной спектр с плавным изменением окраски от красной до фиолетовой. Если источником света служит газоразрядная лампа низкого давления, электрическая дуга или искра между металлическими электродами, когда вещество переводится в атомарное состояние (атомы практически не взаимодействуют), то наблюдается линейчатый спектр – набор спектральных линий, каждая из которых является изображением щели 1 в свете частот, характерных для излучения данного источника.

Линейчатые спектры свидетельствуют о дискретности энергии атомов, т. е. энергия атомов принимает ряд определенных значений E₁, E₂ …, каждое из которых в атомной физике принято представлять в виде энергетического уровня, изображаемого на схеме горизонтальной линией (рис. 3.2). Самый нижний энергетический уровень E₁ валентного (оптического) электрона называется основным и соответствует нормальному (невозбужденному) состоянию атома. Все остальные уровни отвечают возбужденным состояниям атома. Для перевода атома в возбужденное состояние необходимо передать ему определенную энергию (атом поглощает). В возбужденном состоянии атом находится около 10⁻⁸ с и возвращается на более низкие энергетические уровни.

При переходе атома с уровня E_n на уровень E_m (n > m) атом испускает квант излучения
где ν – частота излучения, h = 6,625*10−34 Дж*с – постоянная Планка.

Разрешенные и запрещенные оптические переходы определяются квантовомеханическими правилами отбора. Соответствующие переходы на схеме (см. рис. 3.2) изображаются стрелками.

Атомы каждого химического элемента характеризуются вполне определенным набором дискретных значений энергии и, следовательно, своим линейчатым спектром (набором частот). По наличию совокупности линий элемента в спектре можно судить о наличии данного элемента в составе вещества (качественный спектральный анализ). По интенсивности линий элемента можно судить о его концентрации в веществе (количественный спектральный анализ).

В настоящей работе необходимо по линейчатому спектру ртути построить градуировочный график, определить линейную дисперсию монохроматора УМ-2 во всем диапазоне видимого спектра и построить график зависимости линейной дисперсии от длины волны.




3.3 Описание установки
Оптическая схема монохроматора УМ-2 приведена на рис. 3.3, а внешний вид установки на рис. 3.4.
Источником света 1 является ртутная газоразрядная лампа. С помощью конденсора 2 достигается наилучшее заполнение светом коллиматора 3-4. Маховик 12 позволяет смещать объектив коллиматора 4 относительно щели 3, чем достигается установка щели в его фокусе. На боковой стороне корпуса прибора расположена шкала с нониусом 11, показывающая положение объектива. Входная щель 3 регулируется по ширине микрометрическим винтом 13.

Щель установлена. Изменять положение микрометрического винта 13 не рекомендуется.

Из объектива 4 параллельный пучок лучей направляется на систему диспергирующих призм 5, которая пространственно разделяет лучи различных длин волн и одновременно изменяет направление всего пучка на 90°. Затем лучи света попадают в объектив 6 зрительной трубы, который собирает их в фокальной плоскости 7. Спектр, сформированный в фокальной плоскости, наблюдается с помощью окуляра 8. В этом случае монохроматор работает как спектроскоп.

Для установки спектральной линии в поле зрения окуляра 8 имеется указатель в виде треугольника.

Вывод спектральной линии на указатель производится поворотом диспергирующей призмы 5 при помощи барабана 10. Окуляр 8 путем вращения может устанавливаться по глазу наблюдателя на резкость изображения указателя. Включением тумблеров 14 указатель освещается лампочкой 9, под которой имеется диск с набором светофильтров. Поворачивая диск, можно осветить указатель желтым, красным, зеленым, белым светом. Подсветка может регулироваться по интенсивности вращением рукоятки 15.







3.4. Методика проведения эксперимента и обработка результатов измерения
3.4.1. Методика эксперимента
При вращении барабана 10 (см. рис. 3.4) плавно поворачивается призма монохроматора, вследствие чего спектр перемещается в поле зрения окуляра 8. Для построения градуировочного графика монохроматора УМ-2 выводят последовательно спектральные линии в спектре излучения ртутной лампы под указатель в поле зрения окуляра 8 и производят отсчет α по шкале барабана 10. График зависимости значений α по шкале барабана от длины волны λ в спектре ртути и является градуировочным графиком данного прибора.

Пользуясь им, можно по значениям шкалы барабана определять длины волн в любом спектре, получаемом с помощью этого монохроматора. По графику определяется угловая дисперсия как тангенс угла наклона касательной к градуировочной кривой в определенных точках (соответствующих определенным значениям λ) в пересчете на углы поворота призмы. Затем по формуле (3.5) вычисляют линейную дисперсию и строят график зависимости линейной дисперсии от λ.




3.4.2. Порядок выполнения работы

1. Включите источник света.
2. Проверьте освещение входной щели 3 прибора (см. рис. 3.4) – должно быть равномерно освещено перекрестие защитной крышки. Снимите крышку.
3. Вращая окуляр 8, установите резкое изображение указателя линий.
4. Сфокусируйте спектр вращением рукоятки 12 так, чтобы различался желтый дублет.
5. Вращая барабан 10, просмотрите через окуляр 8 весь спектр от фиолетовых до красных линий.
6. Включите осветительные лампы тумблерами 14.
7. Совместите с острием указателя желтую линию и сделайте по шкале барабана 10 пробный отсчет, который предъявите преподавателю. Если отсчет сделан верно, то можно приступать к измерениям.
8. Последовательно совмещайте с острием указателя линии спектра ртути от красной до фиолетовой и делайте отсчеты по шкале барабана монохроматора, отмечая цвет линии. (Длины волн линий в спектре ртути приведены на лабораторном столе). Затем измерения повторите в обратном порядке от фиолетовой до красной (отсчеты α₂). Результаты запишите в табл. 3.1.
9. Подведите к указателю спектральную линию с неизвестной длиной волны λ_x (по заданию преподавателя) и сделайте отсчет по барабану. Снимите отсчет α₂, подводя ту же линию с другой стороны спектра. Результаты запишите в табл. 3.2 и отметьте цвет линии.

3.4.3. Обработка результатов измерения
3.4.3.1. Построение градуировочного графика