Волны де Броля
|
Построение квантовой механики в начале прошлого столетия началось с гипотезы Луи де Бройля. В 1923-1924г.г. он выдвинул и развил идеи о волнах вещества. К тому времени в оптике уже сложилась парадоксальная, но подтверждаемая опытом ситуация: в одних явлениях (интерференция, дифракция, поляризация, дисперсия)свет ведет себя как волны; в других явлениях (излучение и поглощение света, фотоэффект, эффект Комптона) проявляются с не меньшей убедительностью корпускулярные свойства света, и может быть обосновано рассмотрение световых корпускул - фотонов. Ряд оптических явлений (отражение, давление и преломление света), вообще, может быть объяснен как с точки зрения корпускулярной теории, так и волновой. Анализируя эти обстоятельства, Луи де Бройль выдвинул гипотезу о том, что если свет обладает корпускулярно-волновым дуализмом, то и частицы должны обладать „волново-корпускулярным дуализмом" [1 - 3]. Корпускулярные свойства света (фотонов) характеризуются энергией е и импульсом p', волновые - частотой ω и волновым вектором k' . В соответствии с корпускулярно-волновым дуализмом света имеют место соотношения: ε = ħ ∙ ω (17.1) p' = ħ ∙ k' (17.2) где ħ = 1,055-10-34 Дж∙с - постоянная Планка. По аналогии со свойствами света эти соотношения были постулированы де Бройлем и для микрочастиц вещества. Тогда, в соответствии с формулой (17.2) имеем: p = ħ ∙ k = ħ ∙ ( 2π / λБ ) где λБ – некоторая длина волны, названная впоследствии длиной волны де Бройля. Следовательно, каждой частице вещества массой m, движущейся со скоростью ν, соответствует определенная длина волны λБ : λБ = ( 2π ∙ ħ ) / p = ( 2π ∙ ħ ) / ( m ∙ ν ) (17.3) Рассмотрим некоторые свойства волн де Бройля, вытекающие из соотношений (17.1) – (17.3). Прежде всего, оценим, каков порядок величины длины волны де Бройля для материальных частиц. Пусть мы имеем пучок электронов, ускоряемых напряжением U вольт; если это напряжение невелико, так что можно еще пользоваться формулами классической механики, то скорость электронов (с зарядом e и массой m) определяется из соотношения: ( m ∙ ν2 ) / 2 = ( e ∙ U ) / 300 (17.4) λБ = ( h2 / m ∙ e )1/2 ∙ ( 150 / U )1\2 = 1,225 / U1/2 нм (17.5) Отсюда видно, что для электронов, ускоряемых напряжением 150 В, длина волны де Бройля равна 0,1 нм; это - порядок величины длины волны мягких рентгеновских лучей. Для протонов длина волны де Бройля при той же скорости в √1836 раз меньше. Если скорость электронов велика, то формулы классической механики становятся неприменимыми, и нужно учитывать релятивистскую поправку на зависимость массы от скорости. В таких случаях для определения λБ можно пользоваться следующей приближенной формулой, получаемой при учете релятивистского выражения для кинетической энергии в формуле (17.4): λБ = ( 1,225 / U1/2 ) ∙ (1 - 0,489 ∙ 10-6 ∙ U ) нм (17.6) >Расчеты по формулам (17.5) и (17.6) показывают, что при увеличении ускоряющего напряжения от 10 до 109В длина волны де Бройля для электронов уменьшается от 0,39 до 1,2⋅10-6 нм, а для протонов – от 0,9⋅10-2 до 7,3⋅10-7 нм. Из этого ясно, что для обнаружения интерференции материальных частиц следует пользоваться теми же методами, которые применяются в случае рентгеновских лучей, т. е. интерференцией в кристаллической решетке. Опыты, проведенные в этом направлении Дэви-соном и Джермером в 1927 г., подтвердили правильность такого предположения.
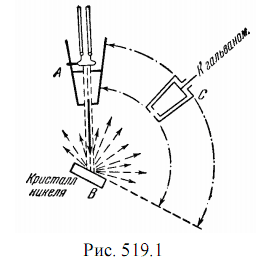
Суть опытов Дэвисона и Джермера состояла в следующем [2]. Параллельный пучок электронов (рис. 17.1) определенной скорости, получаемый при помощи «электронной пушки» А, направлялся на кристалл В; отраженные электроны улавливались коллектором С, соединенным с гальванометром. Коллектор мог устанавливаться под любым углом относительно падающего пучка, оставаясь все время в одной плоскости. Измеряя силу тока коллектора при разных положениях его, можно было судить об интенсивности отражения в различных направлениях. Результат представлялся в виде полярной диаграммы, образцы которой приведены на рис. 17.2. На радиусах-векторах, проведенных под различными углами, откладывались отрезки, пропорциональные интенсивности отражения под соответствующими углами. Оказалось, что если поместить в В (см. рис. 17.1) монокристалл никеля, то при отражении наблюдается резко выраженный селективный максимум, показывающий, что электроны отражаются, следуя оптическому закону: «угол падения равен углу отражения» (см. рис. 17.2, а). Тот же опыт, повторенный с поликристаллической пластинкой никеля, состоящей из множества хаотически расположенных кристалликов, не обнаружил никакой селективности (см. рис. 17.2, б).Опыт с правильным отражением электронов от монокристалла на самом деле представляет точную аналогию интерференционного отражения рентгеновских лучей от кристалла по методу Брэггов. Как известно, рентгеновские лучи испытывают отражение от кристалла только в том случае, если их длина волны и угол скольжения, удовлетворяют формуле Вульфа-Брэггов: m ∙ λ = 2d ∙ sin φ где m = 1, 2, ... - порядок интерференции, d - порядок кристаллической решетки.Эту формулу можно использовать и для анализа интерференционной картины от электронного пучка, полагая λ = λБ , т.е. m ∙ λБ = 2d ∙ sin φ (17.7) Комбинируя формулы (17.5) и (17.7), получаем 1,225 / U1/2 = 1 / m ∙ 2d ∙ sin φ илиU1/2 = 1,225m / ( 2d ∙ sin φ) (17.8) Таким образом, если постепенно менять ускоряющее напряжение U и каждый раз измерять силу тока коллектора (т. е. интенсивность отражения), то, откладывая затем по оси абсцисс U1/2, а по оси ординат—интенсивность отражения l, можно получить кривую с рядом равноотстоящих резких максимумов с расстоянием между максимумами, равным 1,225 / { 2d ∙ sinφ ).
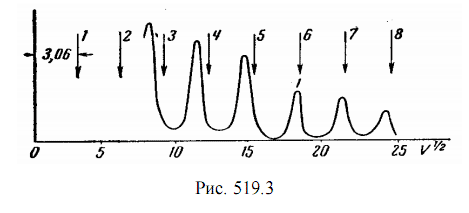
На рис. 17.3 приведена кривая, полученная с монокристаллом никеля при определенных условиях (φ = 80°, d = 0,203 нм). Как видно, периодическое повторение максимумов выражено очень отчетливо. На этом же рисунке стрелками показано положение максимумов, вычисленное по формуле Вульфа—Брэггов (17.7). Сравнение с положением максимумов на экспериментальной кривой показывает, что для высоких значений m (m = 7, 8) имеется точное совпадение; для более низких т обнаруживается расхождение и притом тем большее, чем меньше m. Поскольку это расхождение имеет систематический и закономерный характер, оно показывает, что какой-то фактор не учтен при расчете. Этот фактор есть показатель преломления волн де Бройля. Объяснение смещения максимумов количественно подтверждается вычислением внутреннего потенциала металла из наблюдений над электронной интерференцией. Вычисление это производится следующим образом [2]. Когда электроны попадают внутрь металла, то их импульс меняется, и именно это есть причина преломления электронных потоков с корпускулярной точки зрения. Изменение импульса при попадании внутрь металла объясняется тем, что внутри металла имеется электрическое поле, обусловленное положительными ионами, из которых состоит кристаллическая решетка металла. Если представить себе прямую, проходящую через ряд положительных ионов металла, то при перемещении вдоль этой прямой потенциал, очевидно, должен меняться периодически, так как ионы расположены на равных расстояниях. Однако, можно приближенно заменить этот периодически меняющийся потенциал некоторым средним потенциалом, который и называется внутренним потенциалом металла V. Этот потенциал изменяет, прежде всего, фазовую скорость волн де Бройля. Выражение для фазовой скорости электронных волн вне металла можно получить по аналогии с выражением для фазовой скорости электромагнитной волны. Как известно [3], всякая электромагнитная волна обладает фазовой скоростью νф, которая равна: νф = ω / k Тогда для фазовой скорости волн де Бройля формулы (17.1) и (17.2) дают выражение: νф = ω / k = ( ħ ∙ ω ) / ( ħ ∙ k ) = ε / p = ( m ∙ c2 ) / ( m ∙ ν ) = c2 / ν > c (17.9) то есть волны де Бройля могут распространяться с фазовой скоростью, большей, чем скорость света в данной среде. Полученный результат не должен удивлять, так как на величину фазовой скорости не накладывается никаких ограничений. Выражение для фазовой скорости электронных волн де Бройля (17.9) можно переписать для вакуума в виде [2] νф = ω / k = ( ħ ∙ ω ) / ( ħ ∙ k ) = E / p = E / ( m ∙ ν ) = E / ( m2 ∙ ν2 )1/2 = E / (2m ∙ E )1/2 (17.10) где E - полная энергия электронов в вакууме. Если потенциальная энергия электрона внутри металла есть W, то импульс внутри металла будет pм = ( 2m ∙ ( E - W ))1/2, а фазовая скорость электронных волн внутри металла будет равна νфм = E / pм = E / ( 2m ∙ ( E - W ))1/2 (17.11) Как известно, по определению показатель преломления n для электромагнитной волны на границе раздела двух сред равен n = νф / νфм Тогда для электронных волн де Бройля на границе вакуум-металл показатель преломления n в соответствии с выражениями (17.10) и (17.11) будет определяться по формуле n = νф / νфм = (( E - W) / E)1/2 (17.12) Если принять во внимание, что внутренний потенциал металла V0 положителен, а заряд электрона отрицателен; то тогда потенциальная энергия W - отрицательна: W = - e ∙ V0 Полная энергия Е выражается, как обычно, через внешний ускоряющий потенциал Е = e ∙ V Принимая все это во внимание, получаем из (17.12) выражение для показателя преломления волн де Бройля через внутренний потенциал металла: μ = ( V + V0 )1/2 / V1/2 = ( 1 + ( V0 / V ) )1/2 (17.13) Если рассчитать внутренний потенциал металла с учетом показателя преломления электронных волн де Бройля по формуле (17.13), то получаются значения V0, которые хорошо согласуются со значениями, вычисленными из теории металлов [2]. Это означает, что волны де Бройля для микрочастиц, действительно, испытывают преломление на границе раздела двух сред. Кроме того, это обстоятельство вообще доказывает интерференционный характер отражения волн де Бройля при взаимодействии с веществом, который наблюдался в опытах Девисона и Джермера. Заметим, что рассмотрение преломления волн де Бройля на границе раздела двух сред было проведено на основании использования представлений о фазовой скорости волн де Бройля. Однако следует напомнить, что фазовая скорость волн де Бройля имеет чисто символическое значение и относится к числу принципиально не наблюдаемых величин. Принципиально наблюдаемой величиной является групповая скорость волн де Бройля νГ: νГ = dω / dk = dε / dp Но так как в соответствии с теорией относительности имеет место соотношение: ε = (m02 ∙ c4 + p2 ∙ c2)1/2 то
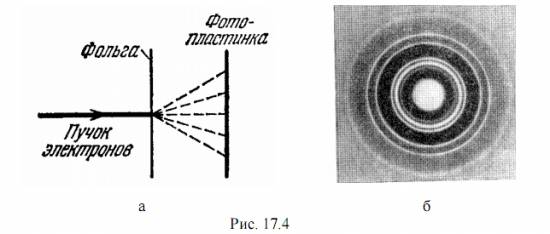
то есть групповая скорость волн де Бройля равна скорости частицы. На первых порах развития квантовой механики была сделана попытка рассмотреть частицы как волновые пакеты. Основания для этого были следующие. Электрон или другая материальная частица не может быть, конечно, плоской гармонической волной, так как подобная волна безгранична, а частица локализована в пространстве и во времени. Но из плоских волн, подбирая соответствующим образом их волновые векторы k', можно строить волновые пакеты, имеющие сколь угодно малое протяжение. Нельзя ли рассматривать частицу как волновой пакет? Подобная гипотеза, казалось бы, находит себе подтверждение в том, что групповая скорость волн де Бройля, то есть именно та скорость, с которой перемещается максимум пакета, как раз равна в соответствии с формулой (17.14) скорости частицы ν. Но при ближайшем рассмотрении эта идея оказывается совершенно неправильной. Решающее возражение заключается в следующем: оказывается, что хотя максимум пакета перемещается со скоростью dω / dk , равной для волн де Бройля ν, сам пакет при движении в реальной диспергирующей среде не сохраняет своей формы и размеров, а постепенно расширяется - расплывается. Как показывает квантово-механический расчет [2], пакет будет удваиваться через промежуток времени выражаемый формулой t = 31/2 ∙ (b2 ∙ m / ħ ) где m - масса частицы; ħ - постоянная Планка, b - полуширина пакета. Для частицы с массой m = 1 г, занимающей протяжение 2 мм (b = 1 мм), соответствующий пакет удваивается через 6∙1017 лет. Но для микрочастицы с массой электрона (m = 0,9∙1027 г) при b ~ 10-12 см и t ≈ 1,6∙10-26 с, то есть пакет, соответствующий электрону, расплывался бы мгновенно, что, конечно, противоречит элементарнейшим наблюдениям. Поэтому представление о распространении микрочастиц в соответствии с распространением волнового пакета не может быть принято в качестве физической интерпретации волн де Бройля. К такому же заключению приводит наблюдение за неделимостью микрочастиц при взаимодействием с веществом (например, для электронов переносящих неделимые заряд и массу). Этим свойством неделимости волны не обладают. На границе двух сред с различной фазовой скоростью волна разделяется на отраженную и преломленную, при прохождении через кристалл она разбивается на ряд дифракционных пучков и т. д. Если бы мы стали рассматривать электрон как суперпозицию волн, то, например, при дифракции очень слабого пучка, когда электроны проходят один за другим через кристалл, каждый дифракционный пучок должен был бы нести только часть электрона, чего на самом деле нет. Если, однако, целостность частиц при таких процессах, как отражение, преломление, дифракция, должна сохраняться, то можно утверждать, что при падении на поверхность раздела двух сред частица либо отразится, либо пройдет во вторую среду. Но в таком случае связь между волнами и частицами может быть истолкована только статистически, а именно, следующим образом: квадрат амплитуды волны в данном месте, измеряющий ее интенсивность, есть мера вероятности найти частицу в этом месте. В случае интерференции волн де Бройля для микрочастиц следует считать, что светлые полосы в сфотографированной интерференционной картине - это места, куда электроны попадают чаще всего; темные полосы - это места, куда они вовсе не попадают. Если теперь применить эти соображения не к собранию большого числа электронов, а к отдельным электронам, то можно также сказать, что вероятность нахождения электрона максимальна там, где амплитуда волнового поля имеет максимальную величину и равна нулю там, где амплитуда равна нулю. Но так как амплитуда может быть и положительной, и отрицательной, а вероятность есть всегда положительное число, то необходимо характеризовать вероятность квадратом амплитуды. Таким образом, связь между распространением волн де Бройля и микрочастиц может рассматриваться только статистически.Гипотеза де Бройля о волнах вещества вскоре была подтверждена экспериментально также опытами Томсона и Тартаковского [1 – 3]. В этих опытах была доказана возможность наблюдения дифракции электронов. Опыты проводились следующим образом В 1928 году Г. П. Томсон и независимо от него П. С. Тартаковский получили дифракционную картину при прохождении электронного пучка через металлическую фольгу (рис.17.4). Г. П. Томсон пропускал тонкий монохроматический пучок быстрых электронов (ускоренных потенциалом от 17,5 до 56,5 кВ) сквозь монокристаллическую фольгу толщиной ∼10-5 см. П. С. Тартаковский использовал поток менее быстрых электронов (ускоренных потенциалом до 1700 В). Опыты осуществлялись следующим образом (см. рис. 17.4, а). Пучок электронов, ускоренный разностью потенциалов, проходил через тонкую металлическую фольгу и попадал на фотопластинку. Электрон при ударе о фотопластинку оказывал на нее такое же действие, как и фотон. Все электроны укладывались на фотопластинке точно по кругу, то есть образовывалась дифракционная картина (рис. 17.4, б). Сходство с полученной в таких же условиях рентгенограммой, было идеальным. Позднее Штерн и его сотрудники показали, что дифракционные явления обнаруживаются также у атомных и молекулярных пучков. Во всех перечисленных случаях дифракционная картина соответствует длине волны, определяемой соотношением (17.3). В опытах Томсона и Тартаковского, а также в опытах Дэвиссона и Джер-мера интенсивность электронных пучков была очень велика. Поэтому можно было предположить, что наблюдаемая дифракционная картина обусловлена одновременно участием в процессе большого числа электронов, а отдельный электрон, проходя через кристалл, не будет обнаруживать дифракции. Чтобы выяснить этот вопрос, российские физики Л. М. Биберман, Н. Т. Сушкин и В. А. Фабрикант осуществили в 1949 году опыт, в котором интенсивность электронного пучка была настолько слабой, что электроны проходили через прибор практически по одиночке. Средний промежуток времени между двумя последовательными прохождениями электрона через дифракционную систему был примерно в 30000 раз больше времени, затрачиваемого одним электроном на прохождение всего прибора. При достаточно длинной экспозиции была получена дифракционная картина, ничем не отличающаяся от той, которая наблюдается при интенсивности пучка в 107 раз большей, но меньшем времени экспозиции (рис. 17.4, б). То есть электроны также укладывались по кругу. Таким образом, было доказано, что и отдельные микрочастицы обладают волновыми свойствами, аналогичными потоку микрочастиц. Добавил: naddy (14.05.2010) | Категория: Квантовая физика Просмотров: 15027 | Загрузок: 0 | Рейтинг: 5.0/4 | Теги: |
| Комментарии (2) | |
|
| |


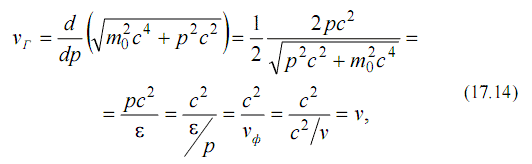
 Круто нах
Круто нах