Обработка результатов тестирования и определение качества теста. Олейник
Составление теста неотделимо от математической обработки результатов тестирования и определения качества создаваемых тестов. Поэтому эти три проблемы объединены в одной главе и будут рассмотрены одна за другой в той последовательности, какая имеет место в ходе работы по созданию теста. Безусловно, вся эта работа должна начинаться с компоновки проекта теста, который в дальнейшем будет называться Тестовым материалом. Последний, применяя методы математической статистики, предстоит превратить в тест хорошего качества. Итак, перед создателем теста стоит задача превращения учебного материала в тестовые задания, которые в дальнейшем будут скомпонованы в нечто целое, т.е. в тестовый материал. При выполнении этой работы следует воспользоваться алгоритмом, который приведен ниже. Однако необходимо отметить, что этот алгоритм несколько отличается от того, который был предложен преподавателями исследовательского центра при МИСиС. Составитель настоящего пособия даже на опыте своей короткой работы с тестовым материалом пришел к выводу, что этапы определения трудности заданий и установления их последовательности в тесте будут выполнены автоматически в ходе статистической обработки результатов тестирования. Поэтому нет необходимости вводить их в алгоритм составления тестового материала. Алгоритм составления тестового материалаСтруктурирование учебного материалаПриступая к составлению теста для проверки знаний по какому-то предмету, необходимо найти ответ, что такое знание предмета, которое необходимо оценить. Если, например, изучаемая дисциплина состоит из ряда разделов, то в определение понятия "знание предмета” должно включаться знание разделов. Затем вводится понятие "знание раздела”, которое раскрывается через названия тем, входящих в раздел. На следующем этапе структурирования материала вводится понятие "знание темы раздела”, которое в свою очередь формируется из названий параграфов (вопросов), составляющих тему. Выделяют также следующие структурные элементы учебного материала (в скобках указаны примерные, часто, применяемое изображения некоторых элементов на логико-структурных схемах):
Установление логических связей между элементами и составление логико-структурных схем.Выделяются следующие типы логических связей:
Затем составляются логико-структурные схемы тем, разделов и всего предмета в целом. Составление тестовых заданий на базе логико-структурной схемыНа логико-структурной схеме выделяются те структурные элементы и логические связи между ними,- знание которых необходимо проверить при помощи теста.„Выделенные элементы и составят содержание тестовых заданий. Выбор оптимальной формы тестовых заданийНаиболее-оптимальным вариантом теста является такой, который состоит из заданий одной формы. Если тест предназначен для проверки знаний по одной теме и состоит из заданий одной формы, то он является гомогенным и по форме и по содержанию. Те тесты, которые охватывают различные темы или даже дисциплины и составлены из заданий различной формы, являются гетерогенными по форме и содержанию. Исходя из поставленной задачи, преподаватель волен выбрать, и форму задания, и форму теста. Например, если надо провести входной контроль только по неорганической химии, то следует выбрать закрытую форму заданий как наиболее простую и легкую. Составленный тест, следовательно, будет гомогенным и по форме, и по содержанию. Если же входной контроль надо провести по физическим методам исследования в химии, то тест должен содержать задания по химии, физике и математике. Однако форма этих заданий должна быть также самой простой, т.е. закрытой, и тест будет гомогенным по форме, но гетерогенным по содержанию. Если же надо составить тест для итогового контроля по всему предмету после завершения его изучения, то такой тест целесообразно составить из заданий всех известных форм, так как надо проверить и знания, и умения, и навыки. Составление плана тестаОптимальное количество тестовых заданий в тесте может колебаться от 30 до 60 при времени тестирования 10-20 минут. Проводят предварительную раскладку заданий по разделам курса, состоящего, например, из 4 разделов, главным из которых является 3-й. Раскладка представлена в табл. 2.1. Таблица 2.1 Распределение тестовых заданий по разделам
В ходе контроля, например, надо проверить умение давать определения /А/, знание формул, законов и принципов /Б/, умение применять знание законов, формул и принципов для решения задач и примеров /В/, умение находить сходство и различие, недостатки и достоинства /Г/, умение представлять материал на графиках и схемах /Д/. Поэтому раскладку заданий конкретизируют по этим умениям (табл. 2.2) Таблица 2.2 Раскладка заданий теста по видам знаний и умений
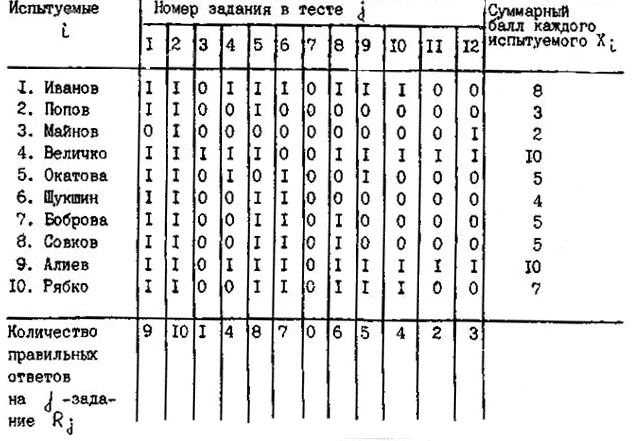
Поскольку в ходе математической обработки примерно 2/3 всех заданий будут забракованы как непригодные, то необходимо с самого начала составить тестовых заданий в 3 раза больше, чем требуется в тесте. Таким образом, для теста длиной в 60 заданий предварительно надо составить около 180 заданий. Проверка теста на большой выборке испытуемыхК обработке результатов тестирования не следует приступать, пока не наберется достаточно большая выборка испытуемых, составляющая примерно 100-150 человек. Составляется матрица тестовых результатов, пример которой для тестового материала из 12 заданий, проверенного на выборке из 10 испытуемых, представлен в табл. 2.3. Конечно, требование к количеству испытуемых здесь не соблюдено ради экономии места. Для оценки знания здесь использована дихотомическая шкала: 1 – знает, 0 – не знает. Таблица 2.3 – Матрица результатов тестирования
Обработка тестовых результатовПредставленная в табл. 2.3 матрица результатов тестирования является неупорядоченной, ибо в ней и испытуемые и задания расположены в случайном порядке. Эту матрицу следует прежде всего упорядочить. Для этого испытуемых надо расположить в таком порядке, чтобы их суммарный балл увеличивался сверху вниз, а задания в свою очередь расположить так, чтобы число правильных ответов на задание Rj понижалось слева направо. При этом из тестового материала сразу выбрасывают те задания, которые не служат цели дифференцирования знаний студентов и являются в этом отношении бесполезными. В данном случае такими заданиями являются второе и седьмое задания. Задание № 2 слишком легкое и на него ответили все испытуемые, задание № 7 слишком трудное, и на него никто не ответил. Получившаяся упорядоченная матрица представлена в табл. 2.4. Помимо уже известных, в табл. 2.4 применены следующие обозначения:
Обе последние величины представляют собой показатель вариации трудности задания, которую мы обозначаем как βj. Из таблицы 2 видно, что в оставшемся тестовом материале имеется два задания, №6 и №7, которые имеют одну величину Rj, что указывает на их одинаковую трудность. Два одинаковых по трудности задания не должны входить в один тест, но только при условии, что они контролируют один и тот же учебный вопрос (тему, раздел). Если же они относятся к различным разделам, и в тесте, кроме них, нет других заданий, контролирующих эти области знания, то такие задания обязательно надо оставить. Таблица 2.4. Упорядоченная матрица тестовых результатов (заданиям,
как и испытуемым, присвоены новые номера. Подчеркнуты ошибочные, стоящие
не на своем месте оценки)
После упорядочения матрицы тестовых результатов вычисляют следующие величины:
При нормальном распределении результатов тестирования В нашем случае Последнее, очевидно, связано с тем, что здесь использована очень малая выборка испытуемых, явно недостаточная для проверки применимости закона нормального распределения. Следующим обязательным шагом при обработке тестовых результатов является вычисление показателей связи тестовых заданий как между собой, так и с суммой тестовых баллов испытуемых Xi. В пособии Аванесова описаны три таких показателя, но здесь будет использован только один обычный коэффициент корреляции Пирсона:
где
Допустим, надо найти
По той же формуле (2.5) рассчитываются коэффициенты корреляции заданий между собой. Например, для связи 5-го задания с 6-м уравнение (2.5) записывается в виде:
Коэффициенты корреляции r здесь представляют собой коэффициенты валидности заданий, характеризующие их пригодность для поставленной цели – дифференциации знаний испытуемых. Все рассчитанные значения r сводятся в корреляционную матрицу, которая для приведенного здесь примера (табл. 2.4) представлена в табл. 2.5. Матрица квадратная, поскольку число строк и столбцов равно числу заданий, а их номера соответствуют номерам заданий в табл. 2.4 Представленные в табл. 2.5 коэффициенты корреляции позволяют произвести объективную выбраковку заданий. Все те задания, для которых коэффициент связи задания с суммарным тестовым баллом испытуемых По величинам Eщё больше информации дают коэффициенты, характеризующие степень связи заданий между собой. Как видно из табл. 2.5, на плохое качество заданий № 3 и 8 указывает наибольшее количество отрицательных коэффициентов в колонках, относящихся к этим заданиям. Средние значения Таблица 2.5. Корреляционная матрица по результатам обработки данных таблицы 2.4.
Наглядно это обстоятельство характеризуют коэффициенты детерминации Если Даже внешний осмотр упорядоченной матрицы, представленной в табл. 2.4, без детального анализа расчетов дает ценную информацию о качестве заданий. Одним из показателей качества заданий является их состоятельность, как и состоятельность испытуемых, о которых можно судить по количеству ошибок в столбцах (состоятельность заданий) и строчках (состоятельность испытуемых). Визуальный осмотр матрицы показывает, что она состоит из двух треугольных матриц, одна из них (верхняя правая) состоит практически из одних нулей, другая (нижняя левая) – из одних единиц. Между указанными треугольными матрицами имеет место достаточно четкая граница. Однако для обеих матриц наблюдаются нарушения, т.е. имеются оценки (подчеркнуты), которые находятся не на своих местах. Чем больше таких нарушений, тем хуже качество теста в целом. Если же анализировать отдельные задания или, отдельных испытуемых, то можно сделать следующие выводы:
Проанализировав тестовые результаты указанными выше способами, с целью улучшения качества создаваемого теста проводят чистку упорядоченной матрицы тестовых результатов: из нее исключают не только несостоятельные задания, но и несостоятельных испытуемых. Если удаление заданий легко обосновать, то удаление испытуемых обосновать значительно труднее, ведь их так просто из учебной группы (класса) не исключишь. Поэтому при исключении испытуемых из тестовых результатов пользуются следующим правилом: из матрицы тестовых результатов исключают не более 5 %, а еще лучше не более 1% испытуемых. Это, с одной стороны, позволяет защитить тест от очень несостоятельных студентов, но с другой также от искусственного завышения качества теста за счет исключения испытуемых, поведение которых не вписывается в рассматриваемую схему. После чистки матрицы 2.4 получают улучшенную матрицу тестовых результатов 2.6, для которой повторяют всю математическую обработку. Корреляционная матрица после чистки тестовой матрицы представлена в табл. 2.7. Даже поверхностное сравнение корреляционных матриц 2.7 и 2.5 показывает, что окончательный тест из 8-ми заданий стал существенно качественнее, чем первоначальный тестовый материал. Об этом свидетельствуют величины Таблица 2.6. Упорядоченная матрица тестовых результатов после удаления несостоятельных заданий и испытуемых
Таблица 2.7. Корреляционная матрица теста после удаления несостоятельных заданий и испытуемых
Структура знанийТест позволяет не только определить уровень знаний испытуемых, но и качественно оценить структуру знаний. Структура знаний – это характер знаний, их полнота, систематичность. Она позволяет более эффективно оценить результаты труда педагога, выявить, что студент не знает и почему, определить студентов с антизнанием. Без всего этого педагог работает вслепую и не может корректировать .учебный процесс в направлении повышения его эффективности. Тот, кто это делать не может, не может быть хорошим педагогом. Структуру знаний характеризует профиль знаний. Например, четыре студента, ответив на тест из 10 заданий, получили суммарный тесто вый балл, равный 5. Однако, студенты имеют разные профили знаний:
За рубежом, особенно в Японии, педагоги обращают внимание не столько на уровень знания, сколько на профиль. Там учебный процесс формируется таким образом, чтобы пробелов в знаниях не было. Правильный профиль не требует пояснений. Обучаемый, обладавший антизнаниями (знает ответы на трудные вопросы и не знает – на легкие), заслуживает того, чтобы педагоги обратили на него внимание и не только выявили причины такого его состояния, но и составили для него индивидуальную программу обучения.. Но среди этих четырех особое беспокойство вызывают 3-й и 4-й студенты, показывающие несистематические знания. Это аварийщики, именно такие специалисты и привели к аварии Чернобыльскую АЭС. Причину каждого неправильного профиля надо анализировать и добиваться ее устранения. Нет сомнения, что неправильный профиль может быть связан с двумя видами причин:
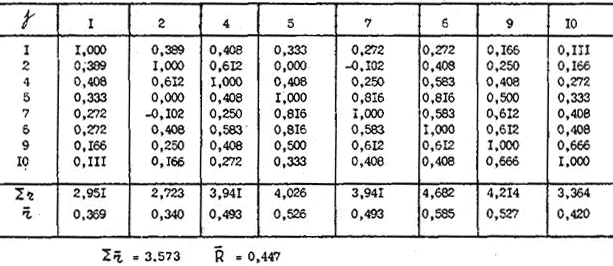
Если окажется, что по какому-то заданию множество студентов (>10%) дают неправильный профиль (по другим заданиям профиль правильный) то такие задания надо исключать из теста, несмотря на хорошие коэффициенты корреляции. Структуированность профиля знаний испытуемых характеризуется числом правильности, профиля или оценкой осторожности (в отношении к уровню знания), которая вычисляется по уравнению:
где
Примеры расчетов:
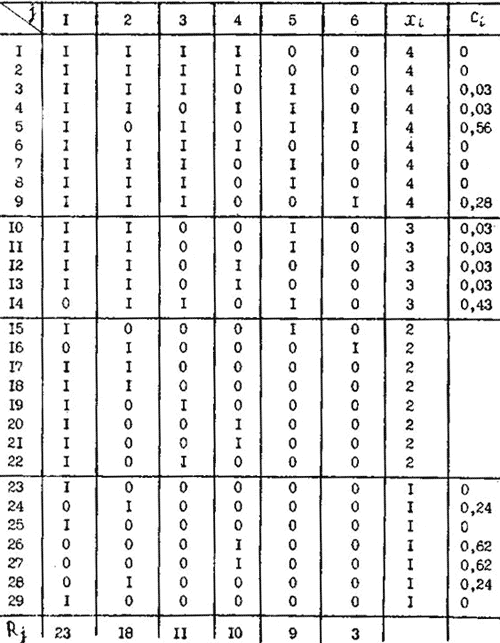
Если Ci=0, то к профилю знаний полное доверие, если же Ci=1 – то полное недоверие. Величину 1-Ci называют индексом структуры знаний, который можно использовать для корректировки тестового балла на неправильный профиль: Хс = Xi(1-Ci). Например, для 5-го студента: Хс = 4 (1 - 0,56) = 1,76 ≈ 2. Таблица 2.8. Упорядоченная матрица тестирования на выборке из 29 человек
Оценка качества тестаНаучно-обоснованный тест – это инструмент измерения, соответствующий установленным стандартам надежности и валидности, определяющим качество теста. Только качественный тест обеспечивает качественный контроль знаний и позволяет составить качественные индивидуальные программы обучения. Валидность теста характеризует пригодность теста для достижения поставленной педагогом цели. В нашем случае – пригодность для дифференциации знаний испытуемых. Надежность же теста связана с точностью измерения уровня знаний. Надежность тестаСуществует множество способов определения надежности. Способ 1Вычисление коэффициента корреляции Пирсона между двумя параллельными тестами на одной и той же выборке испытуемых. Метод был бы прекрасен, если бы не имел существенных недостатков:
Способ 2Корреляция между повторными испытаниями через определенное время одного и того же теста на той же группе. Недостатки очевидны. Способ 3Корреляция тестовых результатов и экспертных опенок. К перечисленным уже недостаткам в этом случае добавляется еще необходимость организации группы экспертов, что увеличивает нагрузку преподавателей. Другие приведенные ниже методы более удобны. Способ 4Расчет коэффициента корреляции по формуле Спирмана-Брауна:
Где rk — коэффициент корреляции между двумя половинками теста. Чтобы обе половинки теста удовлетворяли условию параллельности корреляцию необходимо проверить между четными и нечетными заданий. Пример расчета по этому способу дан ниже для тестовых результатов (табл. 2.4). Эти данные формируются в две параллельные группы, как это показано в табл. 2.9. Таблица 2.9. Применение формулы (2.7) к данным табл.2.4
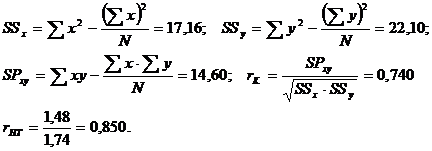 Тест достаточно надежен, поскольку Способ 5
где
Дисперсия ошибок вычисляется по уравнениям:
По данным табл. 2.9
Предложенные выше методы определения надежности основаны на допущениях параллельности и эквивалентности, что далеко не всегда выполняется. Вот почему были найдены методы, которые основаны только на фактах без всяких допущений. Способ 6
где
Для тестовой матрицы 2.4:
Интересно сравнить, как изменяется надежность теста после удаления двух несостоятельных заданий и одного испытуемого. По данным табл. 2.7:
Увеличение rHT было бы еще заметней, если бы число заданий было большим. Например, если k=20, то при том же значении Способ 7Формула KR-20 (авторы Kuder, Richardson, 20-й вариант их формулы):
где
Для данных в табл. 2.4 Для недихотомической шкалы оценок (например, семи или пятибалльной) имеется своя формула надежности:
где Таблица 2.10. Расчет коэффициента надежности рейтинга общественной нагрузки
Способ 8. Надежность теста по Гутману
где Например, для представленной в табл. 2.4 упорядоченной матрицы
Таким образом, как видно, вычисленные различными способами коэффициенты надежности для одного и того же теста различны. Поэтому возникает вопрос, какое же значение коэффициента надежности истинно. Ответ может быть только один: никакое! Ибо нельзя знать точно величину ошибки измерения, но всегда можно получить оценку вероятного значения rHT, что и было выполнено различными способами. Поэтому всегда важно вычислить rHT различными способами. Если rHT вычисленные различными способами, сходны-, то тест надежен (если rHT>0,8). Если же вычисленные значения сильно различаются, то тест не отвечает нужным требованиям, надо искать причину его низкого качества. Для оценки надежности тестов разработаны и другие методы, основанные на применении дисперсионного и факторного анализа. Дисперсионный и факторный анализНе вдаваясь в теорию дисперсионного анализа, затронем лишь практическую сторону его применения для оценки надежности теста. Алгоритм расчета сводится к нескольким этапам:
Все эти вычисления надежности применимы только к гомогенным тестам. Но тесты часто бывают гетерогенными. Их надежность проверяется с помощью факторного анализа. Факторный анализ требует достаточно сложной системы расчетов, которая оформлена в виде программы для ЭВМ и которую невозможно изложить в безмашинном варианте. Говоря о факторном анализе, необходимо отметить, что всегда стремятся свести анализ к возможно меньшему числу факторов. Например, успеваемость можно поставить в зависимость от таких факторов, как пол, жизненные условия, тип оконченной школы (сельская, городская, специальная), время окончания школы и т.д. При анализе может оказаться, что какие-то факторы влияют на уровень знаний, другие – нет. Интерпретация коэффициента надежностиНадежность теста связана с ошибкой измерения соотношением:
Исходя из стандартного отклонения ошибки 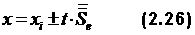 где t – критерий значимости статистики (коэффициент Стьюдента). Его находят из статистических таблиц. Например, при N>120 и р=0,95 t=1,96. Здесь р – надежность, т.е. вероятность риска допустить ошибку. При р=0,95 имеется риск допустить ошибку измерения,. превышающую доверительный интервал, в 5 случаях из 100. Валидность тестовКачество педагогического контроля зависит не только от надежности инструмента измерения, но и от его валидности. Однако в отличие от надежности, определение которой сводится к выбору одной из множества изложенных выше расчетных схем, обоснование валидности теста представляет задачу методологического характера. Процесс валидизации начинается с уточнения цели и конкретных задач педагогического контроля. Если ставится цель проверить знания студентов по определенной дисциплине и при этом неважно, каким методом это будет сделано, то легко понять, что эта цель будет достигнута с помощью зачетов, экзаменов, курсовых и дипломных работ и т.п. Эти методы неравноценны с точки зрения временных затрат, объективности и качества оценки, и потому вопрос о валидности легко переводится в прагматическую плоскость оценки сравнительной пригодности того или иного метода для достижения поставленной цели. Валидность по нормальному распределениюВалидность любого теста можно и нужно оценивать с позиций нормативного типа мышления, при котором любой результат должен быть соотнесен с нормой. Если нет нормы, то трудно сказать, что означает, например, полученный испытуемым Ивановым в каком-нибудь тесте балл 35 – хорошо это или плохо, Если же известно, что нормой является 25 баллов, то оценка 35 принадлежит одному из лучших студентов. В тестовой практике за норму берется средняя арифметическая, результатов тестирования. На требованиях.к норме мы не будем останавливаться, ибо нормирование будет иметь значение при межвузовском контроле знаний и проблема становится актуальной только при разработке тестов для межвузовского контроля. Тест считается валидным, если средний результат тестирования присущ, большей части учащихся, а сами результаты распределяются по нормальному закону. Нормальность распределения достигается путем варьирования числа легких и трудных заданий в тесте. Валидный тест должен содержать подавляющую долю заданий средней трудности, но он обязательно должен иметь и откровенно легкие задания, которые не решает 1 из 100 или даже 1 из 1000 испытуемых, и откровенно трудные задания, которые решает 1 из 100 или 1 из 1000 испытуемых. Валидность теста по распределению легко достигается путем замены заданий, нарушающих нормальность распределения. Валидность по содержаниюЕсли перед тестом стоит цель оценить знание предмета, то задания теста должны охватывать хотя бы все разделы и темы предмета. Когда начинают обрабатывать тест, то зачастую в нем образуются провалы по содержанию, т.е. могут исчезнуть отдельные темы и даже разделы. Перед создателем теста стоит трудная задача заполнить эти пробелы. Ведь при этом необходимо не только втиснуть в задание нужное содержание, но и придать ему ту трудность, которая необходима. Для соответствующего места задания в тесте. При этом задание должно еще и обладать высокой различающей способностью. Валидность по различающей способностиЗадача теста – дифференцировать студентов по уровню знаний. Чем выше дифференцирующая способность теста, тем выше его валидность. Чтобы повысить валидность теста, нужно ввести в него задание с высокой различающейся способностью (РСЗ). Определить РСЗ можно путем вычисления коэффициентов корреляции ответов по каждому заданию с суммой баллов для всех студентов, как это было показано в разд. 2.2.Если r>0,3, то задание обладает достаточной РСЗ. Другой способ определения РСЗ состоит в следующем. Проводится предварительное тестирование достаточно большой выборки испытуемых (N>100), например, при входном контроле, которое при условие нормального распределения результатов позволяет отобрать по 27 % испытуемых в худшую и лучшую группы. Тогда:
где
Здесь n – число правильных ответов. Различающую способность теста можно повысить следующими способами.
Валидность теста и его длинаС увеличением длины теста растет его теоретическая надежность. Но на практике после какой-то определенной (оптимальной) длины и надежность, и валидность теста начинают падать вследствие и усталости испытуемых, и возникающих организационных проблем (организация перерывов и других мероприятий). Поэтому оптимальная длина теста – 40-60 заданий. Существуют различные формулы, связывающие длину и надежность теста.
Валидность и расположение заданийСуществует несколько способов расположения заданий в тесте: в порядке возрастания трудности, расположение по спирали, случайный и специальный порядок. Наиболее валидным в случае гомогенного теста является расположение заданий в порядке возрастания трудности, в гетерогенном – расположение по спирали: сначала находятся наиболее легкие задания по разным дисциплинам, затем задания следующего уровня трудности. Например, для теста по четырем дисциплинам (А, В, С, Д) спиральное расположение заданий будет выглядеть следующим образом: A1B1C1D1A2B2C2D2A3B3………………AnBnCnDn, где индекс внизу соответствует уровню трудности задания. Случайный порядок наиболее валиден в психологических тестах. На специальном порядке мы останавливаться не будем. Способы валидизации тестаИз различных способов определения валидности теста остановимся на одном, наиболее часто применяемом. Это сравнение результатов тестирования с результатами экспертной оценки. Для примера можно привести два следующих варианта этого метода:
Оценка качества тестаКачество теста оценивают отдельно по надежности и валидности, сравнивая экспериментальные данные с требованиями, представленными в табл. 2.11. Так же, как нет единой, раз навсегда установленной, надежности теста, так нет и единой валидности теста. В научных публикациях наряду с информацией о коэффициенте валидности теста, необходимо сообщать о способе его валидизации. Таблица 2.11. Требования к надежности и валидности тестов
© Н.М. Олейник. Фрагмент из учебного пособия по спецкурсу: "Тест как инструмент измерения уровня знаний и трудности заданий в современной технологии обучения. Донецкий государственный университет". Добавил: COBA (13.01.2013) | Категория: СДО Просмотров: 26832 | Загрузок: 0 | Рейтинг: 5.0/1 | Теги: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Комментарии (0) | |

 .
. .
.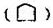 .
.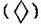 .
. .
. ),
),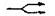 ),
),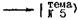 ),
), ).
).
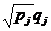 – стандартное отклонение результатов испытуемых по j заданию.
– стандартное отклонение результатов испытуемых по j заданию.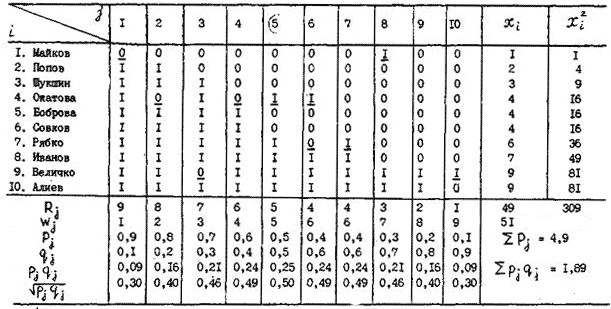
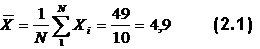
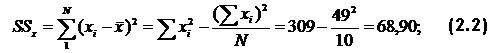
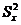 – дисперсия результатов испытуемых;
– дисперсия результатов испытуемых;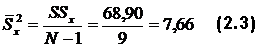
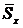 – стандартное (среднеквадратичное) отклонение результатов испытуемых от
– стандартное (среднеквадратичное) отклонение результатов испытуемых от 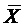 .
.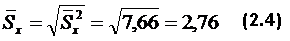
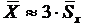 .
.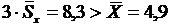 .
.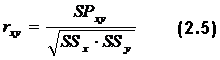
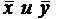 .
.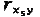 – коэффициент связи 5-го задания c суммой тестовых баллов для каждого испытуемого хi . Тогда xi = y, а SSy = 68,90.
– коэффициент связи 5-го задания c суммой тестовых баллов для каждого испытуемого хi . Тогда xi = y, а SSy = 68,90.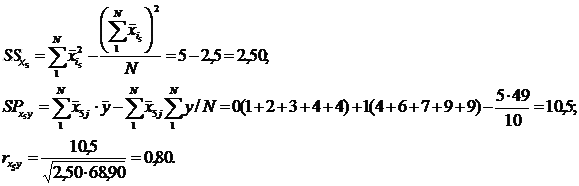
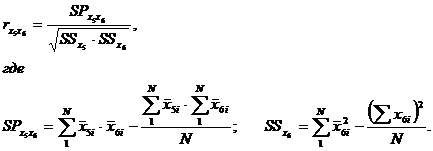
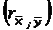 меньше или равен нулю, несостоятельны и непригодны для контроля знаний, поэтому их надо выбрасывать не только из создаваемого теста, но и существенно переделывать и улучшать. Задания же, для которых
меньше или равен нулю, несостоятельны и непригодны для контроля знаний, поэтому их надо выбрасывать не только из создаваемого теста, но и существенно переделывать и улучшать. Задания же, для которых 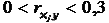 , являются кандидатами на удаление из теста, но не надо спешить удалять их из теста. Может так оказаться, что других заданий в тесте с подобным содержанием нет, и, если это задание выбросить, то окажется, что в тесте по целому разделу (теме, вопросу) образовался пробел. Итак, если тестовое задание уникально, то его стоит в тесте оставить, если даже rxy = 0,1.
, являются кандидатами на удаление из теста, но не надо спешить удалять их из теста. Может так оказаться, что других заданий в тесте с подобным содержанием нет, и, если это задание выбросить, то окажется, что в тесте по целому разделу (теме, вопросу) образовался пробел. Итак, если тестовое задание уникально, то его стоит в тесте оставить, если даже rxy = 0,1.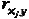 видно, что 3-е и 8-е задания теста из 10 являются наименее пригодными для контроля знаний испытуемых и являются кандидатами на удаление их из теста.
видно, что 3-е и 8-е задания теста из 10 являются наименее пригодными для контроля знаний испытуемых и являются кандидатами на удаление их из теста.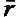 также являются мерой качества задания. Если
также являются мерой качества задания. Если 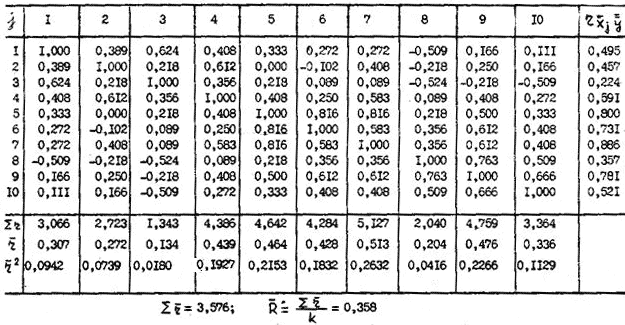
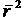 характеризующие меру связи данного задания со всей матрицей, которую можно выразить в процентах (
характеризующие меру связи данного задания со всей матрицей, которую можно выразить в процентах (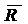 (средние значения средних коэффициентов корреляции для всех тестовых заданий), представленные в табл. 2.5 и 2.7.
(средние значения средних коэффициентов корреляции для всех тестовых заданий), представленные в табл. 2.5 и 2.7.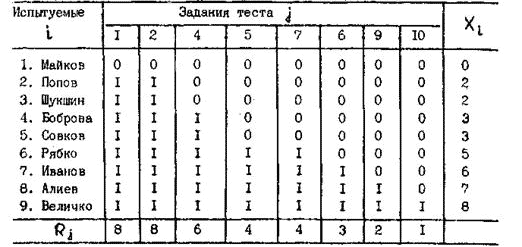
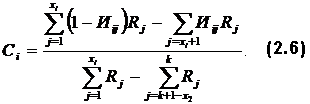
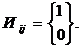
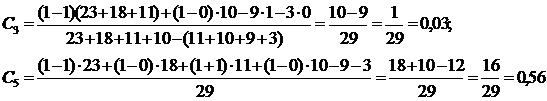
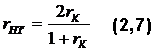
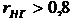 .
.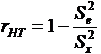
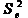 – дисперсия ошибок,
– дисперсия ошибок,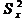 – дисперсия баллов по всему тесту.
– дисперсия баллов по всему тесту.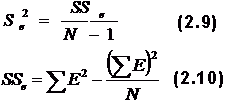
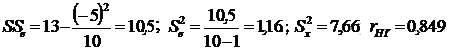
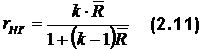
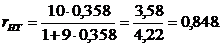
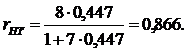
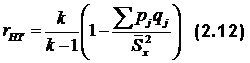
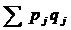 – сумма дисперсий испытуемых.
– сумма дисперсий испытуемых.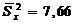 при k = 10, откуда rHT = 0,837. Формула позволяет избежать дополнительных вычислений.
при k = 10, откуда rHT = 0,837. Формула позволяет избежать дополнительных вычислений.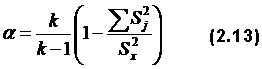
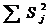 – сумма дисперсий заданий теста, дисперсия суммарных баллов
– сумма дисперсий заданий теста, дисперсия суммарных баллов 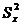 . Пример такого расчета приведен в табл. 2.10, в которой сведен рейтинг в семибалльной шкале (например, сумма баллов семи экспертов) по восьми видам общественной нагрузки (шефская помощь, выступление на собраниях, участие в субботниках и т.д.)
. Пример такого расчета приведен в табл. 2.10, в которой сведен рейтинг в семибалльной шкале (например, сумма баллов семи экспертов) по восьми видам общественной нагрузки (шефская помощь, выступление на собраниях, участие в субботниках и т.д.)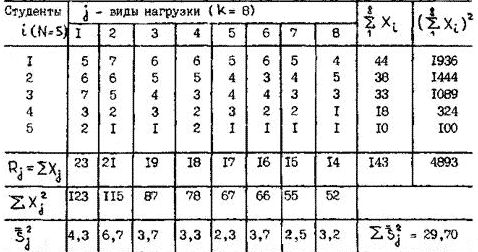
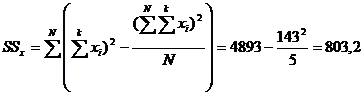
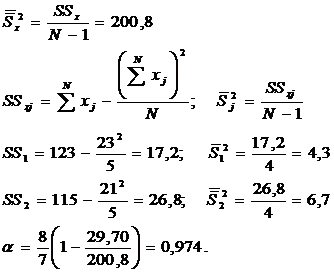
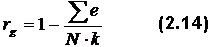
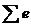 – сумма ошибочных элементов упорядоченной матрицы тестовых результатов.
– сумма ошибочных элементов упорядоченной матрицы тестовых результатов.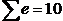 (общее число подчеркнутых элементов). Отсюда:
(общее число подчеркнутых элементов). Отсюда: 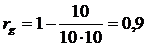
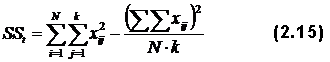
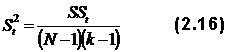
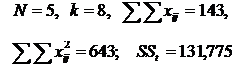
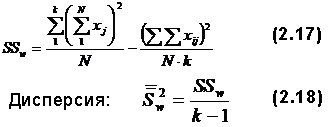
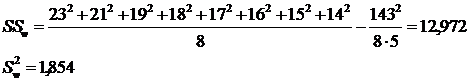
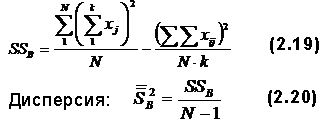
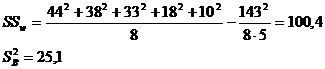
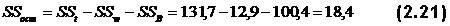
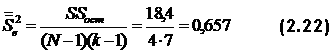
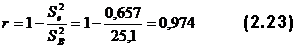
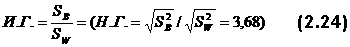
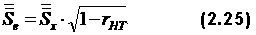
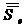 – среднеквадратичное отклонение ошибки,
– среднеквадратичное отклонение ошибки,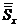 – среднеквадратичное отклонение результатов тестирования.
– среднеквадратичное отклонение результатов тестирования. 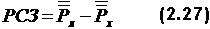
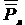 и
и 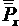 – доли правильных ответов в лучшей и худшей группах:
– доли правильных ответов в лучшей и худшей группах:
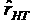 , которая будет получена после
увеличения длины теста в n раз при имеющейся надежности rHT.
, которая будет получена после
увеличения длины теста в n раз при имеющейся надежности rHT.