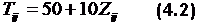Методы сравнения и интеграции результатов педагогического контроля, Олейник
|
Имеется несколько способов выражения тестовых результатов таким образом, чтобы их можно было сравнивать для тестов различной длины, по различным дисциплинам и для разных учебных заведений. Более того эти способы позволяют суммировать тестовые результаты и проводить их накопление, т.е. по сути определять рейтинги испытуемых по всему объему полученных ими знаний. Этим условиям удовлетворяют следующие шкалы оценок тестовых результатов. Шкала ZДля определения оценки по результатам тестирования в шкале Z помимо суммарного бала xi i-го испытуемого по j-й дисциплине (тесту, вузу),- необходимо знать среднее арифметическое баллов для всей группы студентов
Здесь Zij – стандартный результат, представляющий собой нормированное отклонение балла испытуемого от среднего арифметического по тесту. При подчинении результатов тестирования закону нормального распределения, когда
Шкала ТДля устранения указанных выше недостатков шкалы вводится шкала Tij:
Здесь произведение 10Zij округляют до целых чисел, поэтому шкала Т в 10 раз более дифференцирующая знания, чем шкала Zij. Для сравнения этих шкал приведем пример для семи испытуемых:
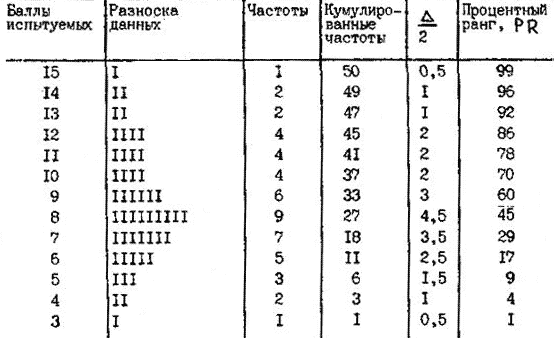
Процентная шкалаПроцентная шкала рассчитывается для большого массива данных. Для примера рассчитаем процентную шкалу по результатам тестирования 50 студентов, получивших следующие баллы: 4, 15, 6, 14, б, 7, 12, 9, 6, 5, 11, 8, 11, 8, 10, 7, 6, 8, 8, 8, 3, 12, 9, 14, 12, 13, 7, 9, 10, 5, 9., 6, 8, 7, 7, 11, 7, 11, 9, 4, 8, 12, 5, 7, 8, 10, 13, 10 (N=50). Прежде всего данные группируются и на этой основе определяется характер распределения тестовых баллов. Характер распределения будет приближаться к нормальному, если N>>100. Поэтому приведенные здесь пример далек от нормального распределения. Группировка данных по так называемым классам выполняется таким образом, чтобы число классов было в пределах от 10 до 15. Для этого определяется размах тестовых результатов (R), который в нашем примере равен R=15-4=11. Таким образом, у нас образуется 11 классов, и в каждый класс, попадает один тестовый балл. Далее строится вспомогательная табл. 4.1, где в первую колонку помешают тестовые баллы испытуемых от большего значения к меньшему сверху вниз. Вторая колонка представляет собой результат разноски исходных данных по баллам (классам). В третью колонку внесены частоты, с какими встречаются в результатах тестовые баллы. В четвертой колонке показаны кумулированные (накопленные) частоты, представляющие собой сумму частот снизу вверх. Таблица 4.1. Вспомогательная таблица для расчета процентного ранга
Так как уровень знаний непрерывно изменяется, мы оперируем дискретными значениями баллов, то необходимо ввести понятие "верхняя и нижняя граница” балла (класса). В нашем примере, например, для балла 12 нижняя граница 11,5 (12-0,5, где 0,5-точность измерения балла, поскольку мы измеряемую величину, т.е. уровень знаний, округляем до целого значения балла с точностью до 0,5), верхняя – 12,5. Именно эти понятия используются для построения шкалы процентных рангов, цель которой узнать, сколько процентов испытуемых показывают результаты, равные интересующему нас баллу или меньше него. Вычислим для примера процентный ранг для тестового балла 5. В пределах от нижней границы балла 4,5 до верхней 5,5 находятся результаты 3 испытуемых. Предполагается, что эти результаты равномерно располагаются в указанном интервале, т.е. от 4,5 до 5,5. Следовательно, в интервале от 4,5 до 5 находится 1,5 долей испытуемых (половина от 3 см предпоследнюю колонку). Таким образом, балл ниже 5 имеют 4,5 (3 + 1,5) долей испытуемых, или 9 %. Балл 3 и ниже имеют 0,5 доли испытуемых, или 1%. Балл 15 имеют 49+0,5=49,5 доли испытуемых, т.е. 99%. Итак, что значит PR=86% для балла 12. Это значит, что знания испытуемого, получившего 12 баллов, превосходят знания 86% студентов группы и он принадлежит к лучшим 14% студентов. Для сравнения общего результата по нескольким тестам процентные данные каждого студента суммируются и суммы сравниваются. Приведение шкал стандартных величин к 11-балльной шкале оценокСуществующая в настоящее время пятибалльная шкала оценок (вернее, даже 4 балльная: неудовлетворительно, удовлетворительно, хорошо и отлично) чрезвычайно не дифференцирующая. Она порождает проблему полупроходных баллов на вступительных экзаменах, не позволяет определить самого лучшего из группы лучших и самого худшего из группы худших. Поэтому наблюдается тенденция к расширению шкалы оценок. В разд. 4.1 уже упоминалась 7-балльная шкала, легко перейти к 9-балльной. Мы предлагаем ввести в практику 11-балльную шкалу, хотя рекомендовать можно и 21-балльную, и 41-балльную и т.д. Однако шкалы, содержащие более 11 баллов, в отличие от 11-балльной шкалы, могут оказаться психологически неудобными и искусственно растянутыми. С нашей точки зрения, в настоящей ситуации, в которой находится педагогика, эта шкала является достаточно дифференцирующей, поскольку позволяет идентифицировать целых 11 групп учащихся вместо 5 при нынешней шкале оценок. 11-балльная шкала вытекает из шкалы логитов, получаемых по самой современной технологии обучения, основанной на латентном анализе. Оказалось, что уровень знаний в шкале логитов лежит в интервале от -6 до +6, что легко трансформируется в 11-балльную шкалу, как это представлено в таблице 4.2. Таблица 4.2. Сравнение различных шкал оценки знаний обучаемых по результатам тестирования
Даже беглого взгляда на табл. 4.2 достаточно, чтобы оценить дифференцирующую способность 11-балльной шкалы по сравнению с ныне существующей 5-балльной, народному образованию, особенно высшей школе, давно пора переходить к более дифференцирующей шкале оценок. © Н.М. Олейник. Фрагмент из учебного пособия по спецкурсу: "Тест как инструмент измерения уровня знаний и трудности заданий в современной технологии обучения. Донецкий государственный университет". Добавил: mauzer (22.01.2013) | Категория: СДО Просмотров: 4770 | Загрузок: 0 | Рейтинг: 0.0/0 | Теги: |
| Комментарии (0) | |

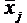 и стандартное отклонение
и стандартное отклонение 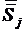 . Тогда оценка Z будет определяться по формуле:
. Тогда оценка Z будет определяться по формуле: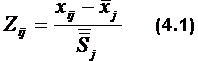
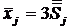 , величина Z непрерывно изменяется от -3 до +3.
, величина Z непрерывно изменяется от -3 до +3.