Метод латентного анализа результатов тестирования. Олейник
Наша официальная педагогика отвергала возможность измерения уровня знаний и интеллекта. На западе широко, у нас меньше, да и то только в последнее время, ведутся исследования по разработке теории таких измерений и по их практическому применению. В данной главе будет рассмотрена не столько теория, сколько практика вычисления: уровня знаний и трудности заданий методами латентного анализа на базе результатов тестирования. Эти оба педагогических параметра, уровень знаний и трудность заданий, являются латентными, скрытными, потому что их нельзя измерить, как длину стола, физическими методами. Эти величины нельзя определить точно сразу. Они оцениваются приблизительно, а затем путем математических действий и итераций приближаются постепенно к их истинному значению. В основе определения указанных латентных параметров лежит представление, что измеряемый параметр, например, сумма тестовых баллов X, состоит из истинного значения Т и ошибки Е (X = T + E). Поскольку X и Е подчиняются нормальному закону распределения, то считается, что и Т также подчиняются нормальному закону. Путем многоступенчатого уточнения ошибки удается определить истинное значение латентного параметра с требуемой степенью точности. Из множества математических моделей для описания вероятности правильного ответа в зависимости от уровня знаний
где D=1,7. Параметр D введен для того, чтобы стандартизировать шкалы вероятностей для различных математических моделей. Для онного i -го испытуемого функция Раша имеет вид:
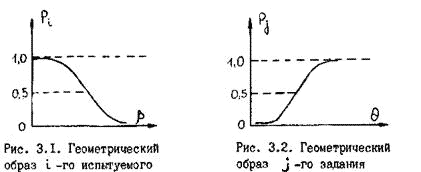
Зависимость вероятности правильного ответа от β, показанная на рис. 3.1, представляет собой геометрический образ i -го испытуемого. Для одного j – го задания функция Раша записывается следующим образом:
Зависимость же вероятности правильного ответа от Ө для j-го задания, представленная на рис. 3.2, является геометрическим образом задания.
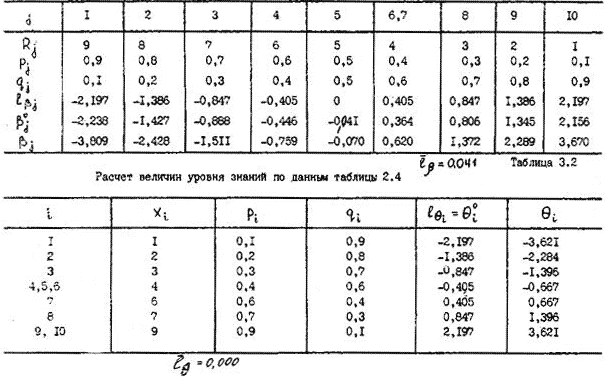
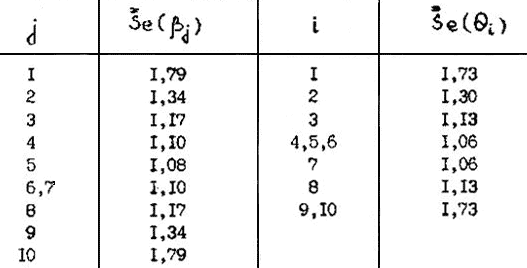
Необходимо обратить внимание, что на кривых, представляющих геометрические образы испытуемых и заданий, имеется одна единственная точка, в которой Ө=β. Это точка перегиба при Р=0,5. Таким образом, наиболее точно значения Өi (и βj) можно измерить в точке перегиба кривых, когда уровень знания равен трудности задания, вероятность правильного ответа наиболее сильно зависит от латентной переменной и позволяет дифференцировать знания испытуемых. Алгоритмы вычисления параметров Өi и βj по однопараметровой модели РашаВсе вычисления будут продемонстрированы на конкретном примере тестирования 10 испытуемых тестом из 10 заданий, представленном в табл. 2.4. В этом случае N = k = 10. Таблица 2.4. Упорядоченная матрица тестовых результатов (заданиям, как и испытуемым, присвоены новые номера. Подчеркнуты ошибочные, стоящие не на своем месте оценки). 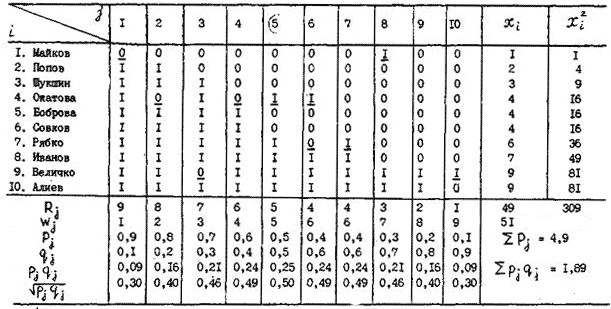 В общем задача сводится к определению Ө и β путем алгоритмических действий и последовательных итераций, исходя из экспериментальных данных тестирования: xi→Өi; где xi – суммарный балл i-го тестируемого, a Rj – сумма правильных ответов для j-го задания. Для измерения этих двух латентных переменных используют одну и ту же единицу измерения – логит: 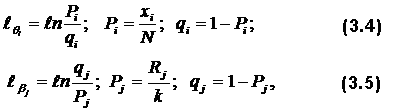 где
Алгоритм вычислений разбивается на ряд этапов:
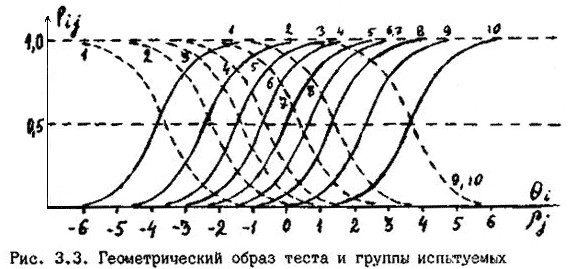
Двух и трехпараметровые модели для нахождения латентных параметров Өi и βjНа рис. 3.3 представлен набор идеализированных математических кривых. Поставим перед собой вопрос, а на сколько они соответствуют действительности? Чтобы получить ответ, следует вычислить экспериментальные значения доли P правильных ответов (при больших N приближающихся к вероятности) на каждое задание в зависимости от уровня знания испытуемых. Однако этого нельзя сделать, если только один испытуемый имеет уровень знания, для которого наблюдается равенство Өi=βj хотя бы в пределах стандартного отклонения ошибки, ибо он дает либо правильный (P=1), либо неправильный ответ (P=0). Причем, оба они далеки от истины, ибо в этой области P~0,5. Чтобы получить достаточно точные значения Р, необходимо иметь большое количество испытуемых с одним и тем же значением Өi. Допустим, у нас 300 испытуемых, а раскладка оценок для теста из 10 заданий такая, какая показана в табл. 3.4. Причем, распределение испытуемых в данном случае близко к нормальному. Для вычисления значений Pj необходима упорядоченная матрица тестовых результатов начало которой для данного случая представлено в табл. 3.5. Таблица 3.4. Результаты тестирования при N = 300 и K = 10
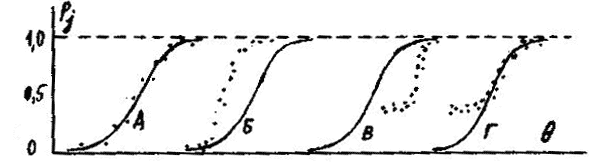
Например, тестовый балл 1 получили 10 человек, и из матрицы очень легко вычислить долю правильных ответов на каждое задание при данном уровне знания (Өi = -3,6). И чем больше группа испытуемых, тем ближе эта доля к вероятности того, что люди с таким уровнем знания дадут правильный ответ на соответствующее задание. Возможны 4 варианта расположения экспериментальных точек относительно идеализированных (усредненных) кривых, показанные на рис. 3.4. Случай А соответствует ситуации, когда однопараметровая модель Раша достаточно хорошо отражает действительность. Все остальные случаи свидетельствуют об обратном, и здесь необходимо переходить к двух- и трехпараметровым моделям. Таблица 3.5. Начало упорядоченной матрицы тестовых результатов при N = 300 и K = 10.
Двухпараметровая модель. Дифференцирующая способность задания ajЕсли точки не совпадают с кривой, как показано на рис. 3.4, то необходимо ввести ещё один параметр:
где aj – параметр, характеризующий крутизну кривой. Если aj=1, то эта зависимость вырождается в однопараметровую модель Раша, если aj>1, то кривая крутая, если aj<0, то пологая. Следовательно, каждое задание характеризуется не только величинами βj, но и aj. Параметр aj – дифференцирующая способность задания.
Крутая кривая задания позволяет лучше дифференцировать тех студентов, уровни знаний которых лежат по разные стороны перегиба. Если точки лежат по одну сторону от перегиба, то знания плохо дифференцируются. Тест должен содержать крутые задания, особенно в средней области трудности, где больше всего студентов, чтобы знания их всех дифференцировать. Например, в случае теста, результаты тестирования по которому представлены в табл. 2.4 и на рис.3.3, вместо одного из заданий №6 или №7 нужно включить несколько крутых заданий, чтобы, дифференцировать знания студентов с обшей суммой баллов, равной 4. При формировании теста в него можно и нужно включать задания с различными значениями и aj, и βj. Если тестируемая группа однородна по уровню знаний, то в тест необходимо брать задание с большой крутизной, если же группа неоднородна, то в тест включаются задания с малой крутизной, но при этом надо стараться, чтобы кривые заданий не пересекались и были расположены по всему пространству. Величина вычисляется при помощи бисериального коэффициента корреляции между баллами i -го задания и суммой индивидуальных баллов всех испытуемых:
Для дихотомической системы оценок бисериальный коэффициент корреляции описывается зависимостью:
Здесь:
Для примера величину 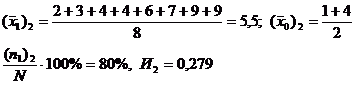
Отсюда:
Задание 2 в тесте не очень хорошее, но и не очень плохое, его можно оставить, если нет лучшего. Имея различную крутизну, задания вносят различный вклад в оценку. Поэтому скорректированный балл описывается уравнением
Здесь значение aj играет роль оптимального весового коэффициента, характеризующего вклад каждого задания в конечный суммарный балл. Трехпараметровая модельДля описания ситуаций, представленных на рис. 3.4В и 3.4Г, двух-параметровой модели уже недостаточно, поскольку здесь необходимо ввести поправку на угадывание, т.е. третий параметр. Тогда уравнение модельной функции будет иметь вид:
где cj – вероятность угадывания ответа для закрытых заданий. Для заданий с двумя ответами cj=0,5, с тремя – 0,33, с четырьмя – 0,25 и т.д. Проблема угадывания правильного ответа может быть решена двумя путями. Первый заключается в введении поправки на угадывание уже в исходные данные при помощи уравнения (1.1). Во втором случае все три параметра (cj, aj и βj) определяются ЭВМ. К сожалению, в настоящее время пока нет формулы, которая позволила бы вычислить скорректированный балл xci с учетом и cj и aj. Метод максимального правдоподобияМетод максимального правдоподобия позволяет при нахождении уровня знаний учесть профиль знаний каждого испытуемого (раздел 2.3). По уже разработанным программам ЭВМ подбирает функцию, характеризующую правдоподобие каждого профиля знаний, а затем таким образом улучшает (подгоняет) значение Өi путем последующей итерации, чтобы функция правдоподобия принимала максимальное значение. Итак, вычисление латентных переменных при помощи новой технологии, основанной на латентном анализе, осуществляется в два этапа:
Информационная функция заданий и тестовПеред новой технологией, основанной на латентном анализе, ставится задача подбора заданий в тест таким образом, чтобы ошибка измерения каждого Өi была наименьшей, т.е. проводится минимизация ошибки:
Этой цели служит информационная функция задания Ij(Ө). Эта функция представляет собой обратное значение стандартной ошибки измерения Өi с помощью данного задания. Эта функция дает количество информации, которую вносит задание в тест. Информационная функция, описывается уравнением:
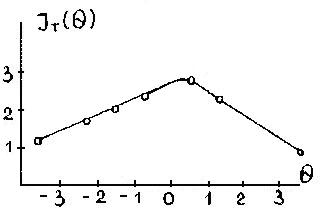
Информационная функция теста представляет собой сумму информационных функций заданий, поскольку они адаптивны:
Из рис. 3.6 видно, что рассматриваемый здесь тест дает максимум информации в точке Ө=0,5, причем, информационная функция мало изменяется в центре, т.е. в области, на которую приходится основная масса студентов. Это свидетельствует о том, что тест обладает низкой разрешающей способностью. Поэтому его надо улучшить, добавив в него задания средней трудности, но обладающие высокой разрешающей способностью.
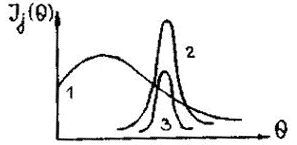
При составлении теста в него необходимо отбирать задачи, вносящие наибольшее количество информации и обладающие высокой разрешающей способностью. Из представленных на рис. 3.7 трех заданий в тест следует включить задание №2, обладающее высокой разрешающей способностью. Задание №3, хотя и обладающее высокой разрешающей способностью, но несущее мало информации, и задание №1 с низкой разрешающей способностью в тест включать нет смысла. Информационная функция теста позволяет вычислить:
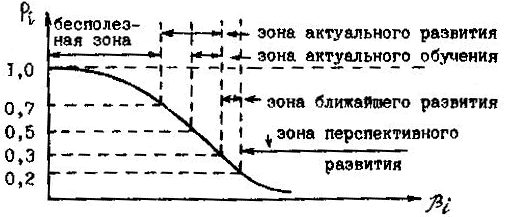
Работа с информационной функцией – завершающий этап технологии составления теста на основе латентного анализа. И этот этап можно выполнить только при помощи ЭВМ. Адаптивный контроль и адаптивное обучениеПредставим себе, что у нас по определенному разделу в результате обработки тестовых материалов отобрано 100 заданий разной трудности во всем диапазоне βj (-6 < βj < 6) и с высокой дифференцирующей способностью. Ясно, что нет смысла давать все задания всем студентам: слабый студент не решит заданий средней трудности и тем более трудных заданий, а сильному незачем решать легкое задание. Особенно необходимо иметь ввиду, что в случае несоответствия трудности задания уровню знаний обучаемого происходит отупление сильных студентов и оболванивание слабых, которые теряют веру в свои силы, получая нерешаемые для них задания. Чтобы уменьшить влияние этих отрицательных факторов контроля, обучаемым надо давать те задания, которые соответствуют (адаптированы) их уровню знаний. Этим и занимается адаптивный контроль. По методике такого контроля ЭВМ (или преподаватель) по таблице случайных чисел выдает учащемуся задание из средней части пакета званий. Если студент не знает ответа, выдается среднее задание из более легкой половины пакета. Если он не отвечает и в этом случае, то выдается одно из средних заданий самой легкой четверти пакета, затем из самой легкой восьмой части и т.д., пока студент не начнет отвечать. Если же студент правильно ответил на задание средней трудности всего пакета, ему выдается среднее задание более трудной половины пакета заданий, затем среднее задание из самой трудной четверти, из самой трудной восьмой части, т.е. до тех пор, пока студент не перестает отвечать. Таким образом, используя минимальное количество заданий, выявляют последнее в ряду трудности задание, на которое данный испытуемый дает правильный ответ. Трудность этого задания и приравнивают к уровню знаний тестируемого испытуемого. На этом контроль заканчивается. Необходимо отметить, что этот контроль пригоден для учащихся с правильным профилем знаний. Чтобы определить профиль, очевидно, необходимо давать короткий тест, среднее задание которого равно уровню знаний испытуемого. Тестовые задания могут и должны выполнять другую свою роль – обучающую. Поэтому их используют в адаптивном обучении, когда обучающий материал соответствует уровню знаний обучаемого. На вопрос, какой трудности задания надо брать при адаптивном обучении, можно ответить, выделяя отдельные зоны на кривой обучаемого, как это показано на рис. 3.8. Если для адаптивного контроля берут задания, для которых соблюдается неравенство 0,7 > Рi ≥ 0,5, то для актуального (адаптивного) обучения берут задания, которым соответствует неравенство 0,5 > Рi > 0,3. Для ближайшего развития планируют задания, соответствующие неравенству 0,3> Рi > 0,2, в перспективе планируют задания, для которых Рi < 0,2. Таким образом, составляется план адаптивного обучения на какой-то ближайший период обучения. Когда он будет выполнен, составляется новый план, адаптированный уже к новому уровню знаний обучаемого.
Эффективность обучения за определенный период можно оценить по уравнению:
где
© Н.М. Олейник. Фрагмент из учебного пособия по спецкурсу: "Тест как инструмент измерения уровня знаний и трудности заданий в современной технологии обучения. Донецкий государственный университет". Добавил: mauzer (19.01.2013) | Категория: СДО Просмотров: 5529 | Загрузок: 0 | Рейтинг: 5.0/1 | Теги: |
| Комментарии (0) | |

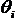 i–го испытуемого и трудности j–го задания
i–го испытуемого и трудности j–го задания 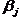 выбрано однопараметровое уравнение Георга Раша:
выбрано однопараметровое уравнение Георга Раша: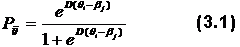
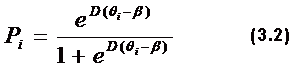
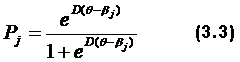
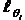 и
и 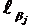 – логиты уровня знаний i-го испытуемого и трудности j-го задания соответственно,
– логиты уровня знаний i-го испытуемого и трудности j-го задания соответственно,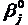 .
.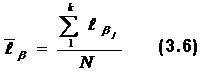
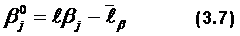
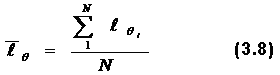
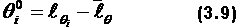
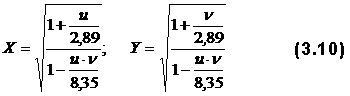
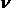 дисперсии β и Ө – соответственно.
дисперсии β и Ө – соответственно.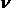 используют уравнения:
используют уравнения: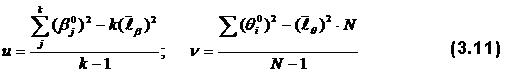
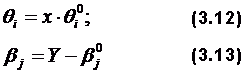
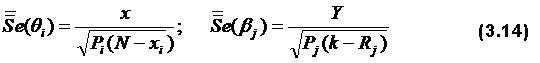


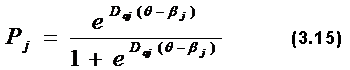
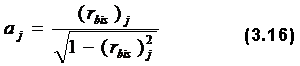
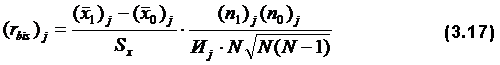
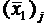 – средний суммарный балл тех испытуемых, которые на j-е задание дали правильный ответ (Xij=1),
– средний суммарный балл тех испытуемых, которые на j-е задание дали правильный ответ (Xij=1),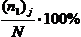 площади под кривой нормального распределения как показано на рис.3.5.
площади под кривой нормального распределения как показано на рис.3.5.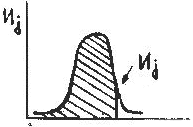
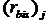 рассчитаем для второго задания табл.2.4. Для этого случая n12=8, n02=2, Sx=2,76,
рассчитаем для второго задания табл.2.4. Для этого случая n12=8, n02=2, Sx=2,76,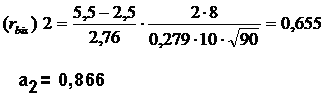
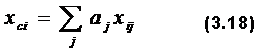
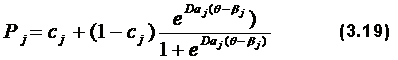

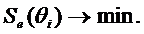
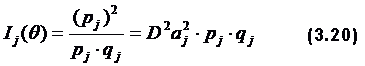
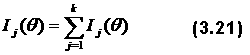

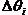 – прирост уровня знания за время t;
– прирост уровня знания за время t;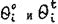 - уровни знании
- уровни знании